
Programarea geometriilor pe masini unelte CN
SISTEME DE COORDONATE
Sistemele de scule ale unei masini-unelte CNC pot executa deplasari care in general sunt dependente de tipul masinii respective.

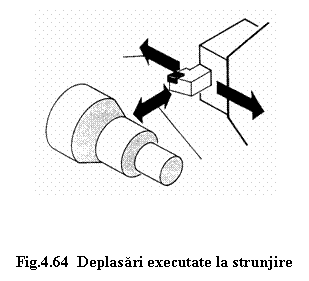
 La prelucrarile prin strunjire aceste deplasari
pot fi deplasari longitudinale
si deplasari de avans (figura
4.64).
La prelucrarile prin strunjire aceste deplasari
pot fi deplasari longitudinale
si deplasari de avans (figura
4.64).
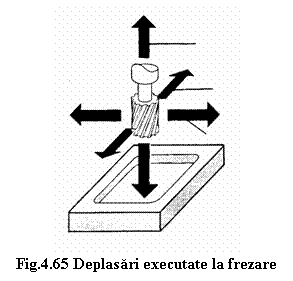
La masinile de frezat acestor doua deplasari li se mai adauga inca o deplasare fundamentala perpendiculara pe primele, denumita deplasare transversala (figura 4.65).
Pentru realizarea preciziei macro si microgeometrice impuse piesei, este strict necesar ca scula sa fie precis controlata din punct de vedere al traiectoriilor pe parcursul acestor deplasari. Toate punctele ce urmeaza a fi parcurse de scula trebuie sa fie definite in mod clar si universal acceptat.
In acest scop a aparut ca o necesitate utilizarea sistemelor de coordonate. Acestea ii permit programatorului sa defineasca traiectoriile sculei si sa le transpuna in realizarea programului.
SISTEME DE COORDONATE CU DOUA AXE
Un sistem de coordonate cu doua axe permite descrierea si definirea precisa a tuturor punctelor (puncte de intersectie, centre ale cercurilor, etc.) care apartin desenului 2D al piesei.
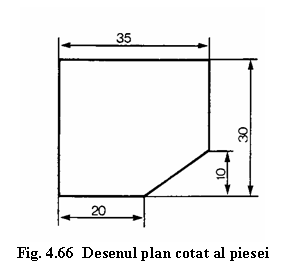
Forma unei piese este descrisa cu precizie atunci cand desenul efectiv al piesei este bine executat si cotat (Fig. 4.66).
Pentru a introduce piesa intr-un sistem de coordonate cu doua axe, suprapunem una sau daca este posibil doua suprafete ale piesei peste axele sistemului (Fig.4.67), forma piesei putand fi descrisa prin determinarea pozitiei cotelor. Putem determina pozitia cotelor citind distanta relativa pe axele X si Y pentru fiecare cota.
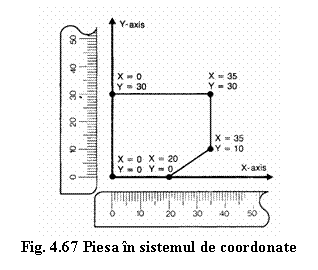
Distanta punctelor masurata pe cele doua axe defineste coordonatele X si respectiv Y.
In aceste conditii forma geometrica si dimensiunile piesei pot fi exprimate intr-un sistem de coordonate cu doua axe, pozitia oricarui punct stabilindu-se in mod exact prin specificarea unei perechi de coordonate (X, Y).
SISTEME DE COORDONATE CU TREI AXE
Cand desenul unei piese este plasat intr-un sistem de coordonate bidimensional, orice punct de pe desen poate fi determinat prin indicarea celor doua coordonate ale sale.
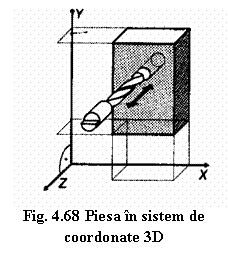 De exemplu centrul alezajului
din figura 4.68 are coordonatele X=35 si Y=45 iar diametrul acestuia Ф10,
elemente ce rezulta din sistemul de coordonate bidimensional. Dar oare
este suficient pentru definirea corecta a alezajului ?
De exemplu centrul alezajului
din figura 4.68 are coordonatele X=35 si Y=45 iar diametrul acestuia Ф10,
elemente ce rezulta din sistemul de coordonate bidimensional. Dar oare
este suficient pentru definirea corecta a alezajului ?
Raspunsul este negativ, trebuie sa stim cat de adanc este alezajul. Nu se pune doar problema pozitionarii alezajului pe suprafata piesei ci si cea a adancimii acestuia. Miscarea burghiului din figura 4.68 nu poate fi descrisa numai de catre coordonatele X si Y, fiind necesara inca o coordonata pentru precizarea adancimii gaurii, adica coordonata Z.
In general in cazul operatiilor de frezare sau gaurire este necesar sa ne imaginam piesa tridimensional.
Pentru a putea gandi configuratia geometrica si dimensionala a unei piese in maniera "tridimensionala" avem nevoie de un sistem de coordonate cu trei axe.
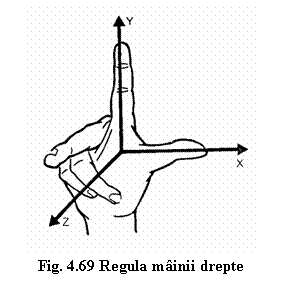
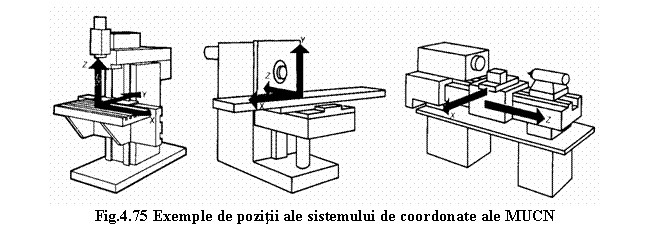
Sistemul de axe tridimensional pentru MUCN este un sistem triortogonal ce respecta regula mainii drepte (figura 4.69). Axele X si Z sunt orientate dupa degetul mare respectiv mijlociu si formeaza planul orizontal al triedrului. Axa Y este perpendiculara pe primele doua si este orientata dupa degetul aratator.
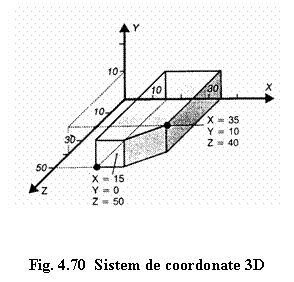
Cele trei coordonate X, Y, Z ale unei piese se obtin prin indicarea pozitiilor cotelor pe cele trei axe (figura 4.70) .
Fiecare axa are valori pozitive si negative. Sensurile pozitive ale axelor sunt cele indicate in figura 4.69.
2 SISTEMUL DE COORDONATE AL MASINII UNELTE
Sistemul CNC al masinii-unelte converteste valorile coordonatelor punctelor ce determina traseul sculei aschietoare din programul NC in:
deplasari ale sculei (figura 4.71);
Avansul sculei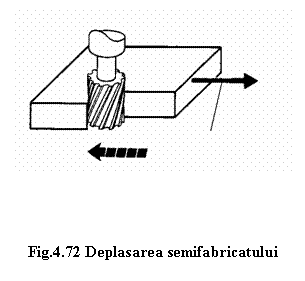
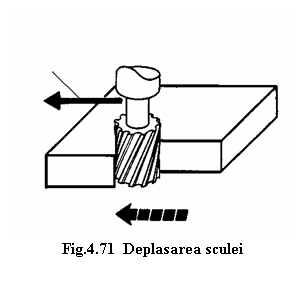 si/sau deplasari ale semifabricatului (figura 4.72);
si/sau deplasari ale semifabricatului (figura 4.72);
Avansul semifabricatului
Directia de deplasare este aceeasi in ambele cazuri.
In toate situatiile, prelucrarea unei piese cu un program NC necesita un sistem de coordonate legat de masina-unealta CNC.
 Asa cum am precizat la programare este necesara asumarea
ipotezei ca piesa este stationara iar scula
executa miscarile in sistemul de coordonate. Acest mod de
percepere al problemei este denumit "deplasarea relativa a sculei" si face
posibil clar si in mod universal acceptat controlul sculei prin indicarea
coordonatelor.
Asa cum am precizat la programare este necesara asumarea
ipotezei ca piesa este stationara iar scula
executa miscarile in sistemul de coordonate. Acest mod de
percepere al problemei este denumit "deplasarea relativa a sculei" si face
posibil clar si in mod universal acceptat controlul sculei prin indicarea
coordonatelor.
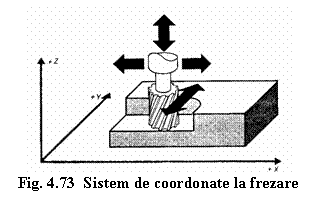
La operatia de frezare (figura 4.73) chiar daca deplasarea dupa axa Y este in general realizata de masa masinii si implicit de semifabricat, la programare se considera deplasarea sculei.
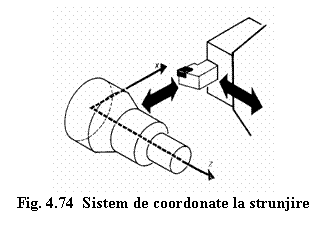
Si in cazul operatiilor de strunjire (figura 4.74) se porneste de la aceeasi ipoteza a piesei stationare. Piesa este pozitionata in sistemul de coordonate astfel incat axa Z sa coincida cu axa arborelui principal si implicit al piesei (axa de rotatie) si axa X corespunde cu directia de avans transversal al sculei.
Axa transversala este axa X reprezentand in general valorile diametrelor iar cea longitudinala este axa Z, reprezentand lungimea fiecarui tronson ce urmeaza a fi prelucrat.
Ca regula generala privind sistemul de axe ale MUCN axa Z coincide cu axa arborelui principal al masinii, celelalte doua axe fiind orientate respectand regula mainii drepte.
Exista situatii cand in cadrul sistemului de coordonate este avantajoasa descrierea pozitiei unui punct utilizand unghiurile axelor de rotatie si coordonatele polare.
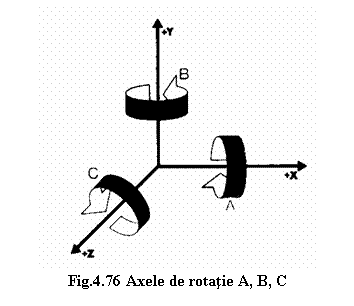 Rotatia in jurul axelor de
coordonate se identifica prin unghiurile axelor de rotatie A, B, si C
(figura 4.76).
Rotatia in jurul axelor de
coordonate se identifica prin unghiurile axelor de rotatie A, B, si C
(figura 4.76).
Directia de rotatie este pozitiva (+) cand se realizeaza in sensul acelor de ceasornic atunci cand privim din punctul de coordonate zero in directia pozitiva a axelor.
Un exemplu de utilizare a unghiului de rotatie este programarea coordonatelor polare intr-un singur plan.
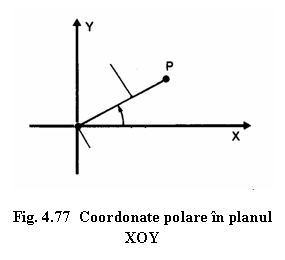
 Coordonatele polare ale unui punct (vezi punctul P din Fig.4.77) sunt
date de distanta dintre punctul programat si punctul zero al
sistemului de coordonate (distanta R=30 mm) si unghiul dintre segmentul OP
si o axa a sistemului de coordonate (de exemplu unghiul C=30 facut
cu axa X).
Coordonatele polare ale unui punct (vezi punctul P din Fig.4.77) sunt
date de distanta dintre punctul programat si punctul zero al
sistemului de coordonate (distanta R=30 mm) si unghiul dintre segmentul OP
si o axa a sistemului de coordonate (de exemplu unghiul C=30 facut
cu axa X).
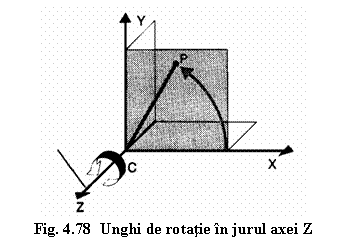
Unghiurile unui sistem polar de coordonate se identifica cu A, B sau C. corespunzatoare axelor de rotatie in sensul carora se masoara:
- Daca punctul apartine planului XOY al sistemului de coordonate, unghiul polar de coordonate se identifica cu unghiul de rotatie in jurul axei Z: C (figura 4.78);
- Daca punctul apartine planului YOZ al sistemului de coordonate, unghiul polar de coordonate este egal cu unghiul de rotatie in jurul axei X: A;
- Daca punctul apartine planului XOZ al sistemului de coordonate, unghiul polar de coordonate este egal cu unghiul de rotatie in jurul axei Y: B;
3 PUNCTUL « ZERO » SI PUNCTUL DE REFERINTA
Asa cum se preciza in subcapitolul anterior la prelucrarile pe MUCN deplasarile sculei sunt controlate prin sisteme de coordonate. Pozitia precisa a sculelor in raport cu masina se stabileste utilizand asa numitul punct zero.
Pe langa punctul zero, in general masinile CNC mai au un numar de puncte de referinta care pot fi utilizate atat in programare cat si in executarea operatiilor.
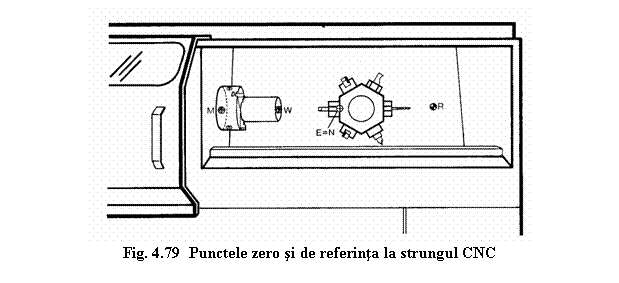 In figura 4.79 sunt punctele: zero si de
referinta, in cazul unui strung cu comanda numerica. Punctul zero poate fi asociat
masini si se va numi «punctul zero masina » M sau
piesei si se va numi punctul « zero piesa » W;
In figura 4.79 sunt punctele: zero si de
referinta, in cazul unui strung cu comanda numerica. Punctul zero poate fi asociat
masini si se va numi «punctul zero masina » M sau
piesei si se va numi punctul « zero piesa » W;
Punctele de referinta prezentate sunt: punctul de referinta R utilizat la initializarea miscarilor si punctul de referinta al sculei E utilizat la reglarea sculelor. Aceste aspecte vor fi prezentate pe larg in continuare:
![]() PUNCTUL
« ZERO MASINA » M
PUNCTUL
« ZERO MASINA » M
A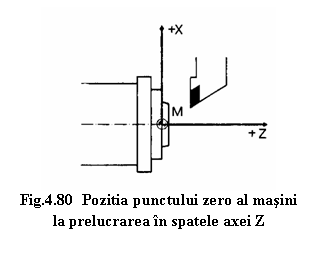
Fiecare sistem CNC al unei masini-unelte
are un sistem de coordonate. Acest sistem este definit de deplasarile
posibile si de un sistem asociat de masurare al acestora.
Punctul zero M al masinii este un punct particular al acesteia si intotdeauna este specificat de producatorul masinii in documentatia tehnica a acesteia. Acesta este punctul zero din sistemul de coordonate al masinii si punctul de plecare
 pentru toate celelalte sisteme
de coordonate si puncte de referinta .
pentru toate celelalte sisteme
de coordonate si puncte de referinta .
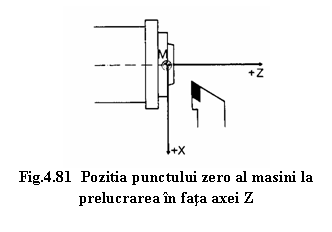
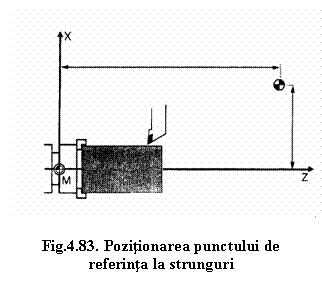
La strunguri, punctul zero al masinii este situat pe axa Z in centrul suprafetei frontale a arborelui principal. Axa arborelui principal (linia de centru) reprezinta axa Z, iar axa perpendicularǎ pe directia arborelui principal in plan orizontal determina axa X (figurile 4.80, 4.81).
 Directiile axelor pozitive X si Z marcheaza
zona de lucru.
Directiile axelor pozitive X si Z marcheaza
zona de lucru.
Cand scula se indeparteaza de semifabricat, atat pe axa Z cat si pe axa X se va indrepta in directie pozitiva.
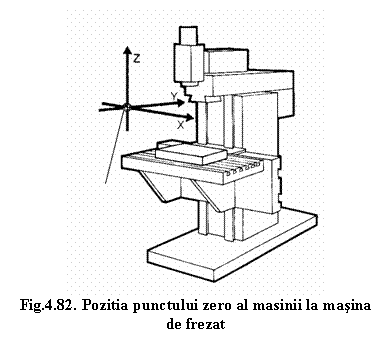
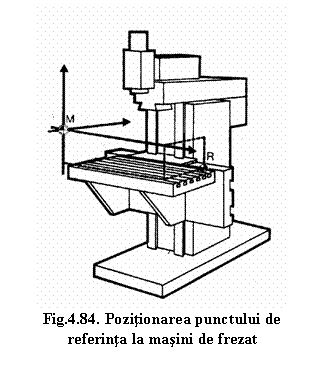
La masinile de frezat (figura 4.82), pozitia punctului zero al masinii variaza, in general, de la producǎtor la producǎtor.
Pentru a cunoaste cu exactitate pozitia punctului zero al masinii ca si directiile si sensurile axelor de avans trebuie consultate cu atentie instructiunile prevǎzute in cartea masinii.
![]()
![]()
PUNCTUL DE REFERINTǍ R AL MASINII
![]() In momentul pornirii
MUCN sculele se aflǎ intr-o pozitie oarecare. Pozitie pe care
initial nu o cunoastem. De aceea este necesara o deplasare
intr-un punct bine stabilit a carei coordonate fata de ZERO
masina sa le cunoastem foarte bine urmand ca apoi dupa
aceasta initializare sa putem aborda faza de lucru ce urmeaza
a fi executata cu indicarea
continua a pozitiei curente de deplasare a sculelor in raport cu punctul
de referintǎ.
In momentul pornirii
MUCN sculele se aflǎ intr-o pozitie oarecare. Pozitie pe care
initial nu o cunoastem. De aceea este necesara o deplasare
intr-un punct bine stabilit a carei coordonate fata de ZERO
masina sa le cunoastem foarte bine urmand ca apoi dupa
aceasta initializare sa putem aborda faza de lucru ce urmeaza
a fi executata cu indicarea
continua a pozitiei curente de deplasare a sculelor in raport cu punctul
de referintǎ.
Asadar punctul de referintǎ R (reprezentat prin ) serveste la gradarea si controlarea sistemului de mǎsurǎ al sǎniilor si deplasǎrilor sculei.
Pozitia punctului de referinta este determinatǎ in prealabil cu precizie pe fiecare axa astfel, coordonatele punctului de referinta au intotdeauna aceiasi valoare numericǎ precisǎ, relativ la punctul zero al masinii.
Dupa initierea sistemului de control, punctul de referinta trebuie intotdeauna sa fie apropiat de axe pentru etalonarea sistemului de mǎsurare a deplasǎrii.
 In cazul accidental in care toate datele
pozitionǎrii curente a saniei respectiv a sculelor se pierd, de exemplu,
in urma unei intreruperi de curent, masina va fi repozitionata in
raport cu punctul de referinta pentru a restabilii valorile pozitiei
initiale.
In cazul accidental in care toate datele
pozitionǎrii curente a saniei respectiv a sculelor se pierd, de exemplu,
in urma unei intreruperi de curent, masina va fi repozitionata in
raport cu punctul de referinta pentru a restabilii valorile pozitiei
initiale.
Masinile unelte echipate cu sisteme de mǎsurare absolutǎ a deplasǎrilor nu necesitǎ un punct de referintǎ deoarece valorile precise ale deplasǎrilor pe axe pot fi citite direct si oricand in coordonate absolute.
 Oricum, majoritatea masinilor CNC utilizeaza
sisteme incrementale de mǎsurare a
deplasǎrilor care necesitǎ un punct de referinta pentru
etalonarea deplasǎrilor.
Oricum, majoritatea masinilor CNC utilizeaza
sisteme incrementale de mǎsurare a
deplasǎrilor care necesitǎ un punct de referinta pentru
etalonarea deplasǎrilor.
La anumite tipuri de masini (de exemplu la masinile de frezat) sistemul de masurare poate fi de asemenea etalonat prin pozitionarea fatǎ de punctul zero al masinii, fǎrǎ a mai fi necesar punctul de referintǎ.
Cu toate acestea, in cele mai multe cazuri punctul zero al masinii nu poate fi atins atunci cand sculele si piesele semifabricate sunt in pozitie de lucru. In consecintǎ, trebuie utilizat si un punct de referintǎ.
![]()
PUNCTUL "ZERO AL PIESEI" W
![]()
Punctul zero W al piesei (reprezentat prin ) determinǎ sistemul de coordonate al piesei relativ la punctul zero M al masinii.
Punctul de zero al piesei este ales de cǎtre programator si introdus in sistemul CNC la setarea initialǎ a masinii unelte cu comandǎ numericǎ.
Zero piesa
Teoretic
pozitia punctului zero al piesei poate fi aleasǎ de programator oriunde pe suprafata piesei.
Totusi, este recomandabilǎ plasarea punctului zero al piesei astfel
incat dimensiunile din desenul piesei sǎ fie usor adaptate la
valorile coordonatelor.
In figura 4.85 se prezintǎ douǎ exemple de stabilire a punctului zero piesǎ in cazul reperelor strunjite.
Zero piesa Zero piesa Zero
masina
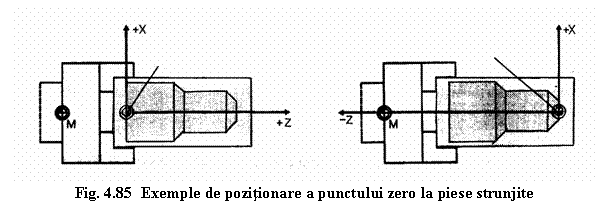
Ca si regulǎ este bine ca punctul zero
al piesei sǎ fie plasat de-a lungul axei arborelui principal care este
si axa piesei, pe una din suprafetele frontale ale reperului asa
cum aratǎ acesta dupǎ prelucrare. (Fig.4.85.)
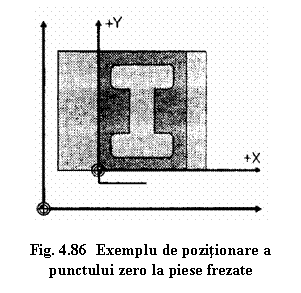 In cazul reperelor frezate, este in general recomandat
sǎ se foloseascǎ ca punct zero al piesei, un unghi drept al piesei,
fatǎ de care sunt date
majoritatea cotelor din desenul de excutie (Fig.4.86).
In cazul reperelor frezate, este in general recomandat
sǎ se foloseascǎ ca punct zero al piesei, un unghi drept al piesei,
fatǎ de care sunt date
majoritatea cotelor din desenul de excutie (Fig.4.86).
Punctul zero al piesei mai este denumit punctul zero program.
Zero piesa
Douǎ reguli de care trebuie sǎ se
tinǎ cont la alegerea punctului zero al piesei sunt:
a) valorile coordonatelor sǎ poatǎ fi luate pe cat posibil, direct din desen.
b) orientarea la fixare, pregǎtirea si verificarea, sistemul de masurare al deplasǎrii sǎ poatǎ fi efectuate usor.
PUNCTE DE REFERINTA ALE SCULEI
Lungimea sculei Lungimea sculei Lungimea sculei
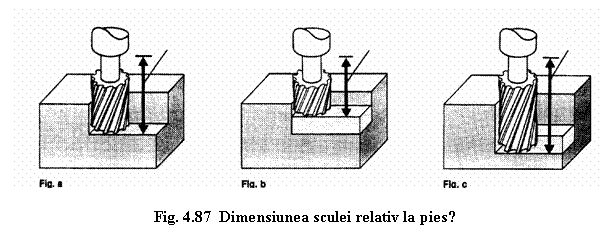 Pentru realizarea conturului piesei se programeazǎ
intotdeauna deplasarea muchiei aschietoare a sculei relativ la piesǎ.
Pentru realizarea conturului piesei se programeazǎ
intotdeauna deplasarea muchiei aschietoare a sculei relativ la piesǎ.
Lungimea sculei Lungimea sculei
Deplasarea
programatǎ a sculei trebuie sǎ fie in concordanta cu
lungimea proprie a sculei (Fig.4.87.). Daca sistemul de control percepe o
lungime gresita a sculei, conturul dorit nu se va realiza. Daca
lungimea proprie a sculei este prea micǎ (Fig.4.87 b.) se va inlǎtura
material insuficient. Daca lungimea proprie a sculei este prea lunga
(Fig.4.87 c.) se va inlǎtura prea mult material.
 In consecintǎ,
dimensiunile sculei trebuie mǎsurate si raportate la un sistem de
referintǎ. Datele
referitoare la dimensiunile sculei sunt stocate in sistemul de control al
masinii.
In consecintǎ,
dimensiunile sculei trebuie mǎsurate si raportate la un sistem de
referintǎ. Datele
referitoare la dimensiunile sculei sunt stocate in sistemul de control al
masinii.
Asadar la prelucrarea unei piese, este esential controlul asupra varfului sculei sau asupra muchiilor aschietoare ale sculei aflate in stransǎ relatie cu pozitionarea piesei in raport cu originea masinii.
Din moment ce sculele au forme si dimensiuni diferite, dimensiunile precise ale sculei trebuie sǎ fie stabilite in prealabil si introduse in sistemul de control.
Dimensiunile sculei sunt legate de
un punct fix al sculei respectiv portsculei, stabilit inaintea montǎrii.
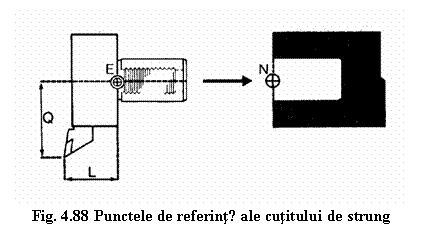
Acesta este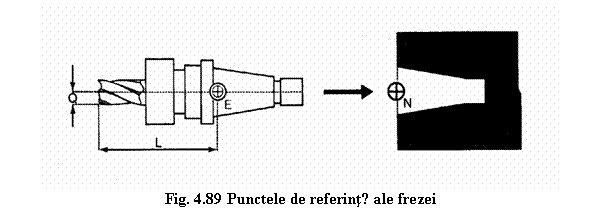 punctul de referinta E al sculei care este localizat
relativ la un punct bine precizat pe portsculǎ N (figurile 4.88, 4.89).
punctul de referinta E al sculei care este localizat
relativ la un punct bine precizat pe portsculǎ N (figurile 4.88, 4.89).
Aceste douǎ punct fixe permit pozitionarea sculei fǎrǎ ajutorul masinii unelte cu comanǎ numericǎ.
In figura 4.88 se prezintǎ de asemenea schema de reglare a cutitelor de strung iar in figura 4.89 schema de reglare a frezelor. In cazul cutitelor de strung cotele de reglare in raport cu punctul E sunt Q respectiv L mǎsurate pe cele douǎ axe X respectiv Z. Pentru freze, cotele de reglare sunt date de distanta L intre punctul E si suprafata frontalǎ a frezei si Q intre punctul E si un punct de pe suprafata circumferintei exterioare a frontalului frezei.
Omologul punctului de referintǎ al sculei pentru portscula este punctul N (figura 4.88, 4.89) numit punctul de referintǎ al portsculei
In stare montatǎ, a sculei in portsculǎ, punctele E si N coincid.
Pentru o determinare precisa a pozitionarii varfului sculei relativ la punctul zero al masinii, controlul foloseste punctul de referintǎ a portsculei impreuna cu datele ce fac referintǎ la dimensiunile sculei.
PUNCTE DE REFERINTǍ ALE SANIEI SI ALE CAPULUI REVOLVER
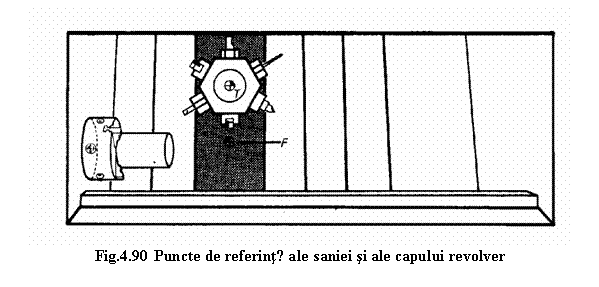 In cazul masinilor cu
capete revolver si respectiv magazii de scule (strunguri cu comandǎ
numericǎ, centre de prelucrare) pentru
realizarea programului va fi necesarǎ precizarea nu numai a punctului de
referintǎ a portsculei dar si alte puncte de referinta
legate de miscarea componentelor purtǎtoare de sculǎ ale
masinii.
In cazul masinilor cu
capete revolver si respectiv magazii de scule (strunguri cu comandǎ
numericǎ, centre de prelucrare) pentru
realizarea programului va fi necesarǎ precizarea nu numai a punctului de
referintǎ a portsculei dar si alte puncte de referinta
legate de miscarea componentelor purtǎtoare de sculǎ ale
masinii.
Se defineste astfel punctul de referintǎ T al capului revolver, care este un punct fix pe cap si este in general localizat in centrul de simetrie al acestuia. Un alt punct important este punctul F situat pe sania portsculǎ intr-o pozitie determinata precis.(figura 4.90)
DEPLASǍRI
Realizarea profilului pieselor prelucrate prin aschiere presupune realizarea deplasǎrii sculei relativ la semifabricat pe niste traiectorii bine stabilite. Deplasarile posibile ale sculei sunt dependente de tipul masinii si de tipul sistemului de control.
In functie de tipul echipamentului CNC deplasǎrile pot fi comandate independent pe axe, pot fi compuse in scopul obtinerii unor deplasǎri liniare sau circulare, altele decat cele ce coincid cu axele masinii.
Executarea de miscǎri controlate ale sculei realizate prin sistemul numeric de control, cu ajutorul calculelor interne, poartǎ denumirea de "interpolare".
In cadrul acestui subcapitol se prezintǎ modul in care aceste miscǎri fundamentale ale sculei pot fi controlate prin interpolare la masinile CNC.
INTERPOLAREA LINIARA
Tinta Start
Deplasarea
unei scule de la un punct de start la un punct tinta dat (figura 4.91)
in conditiile in care se face de-a lungul unei linii drepte, se
numeste interpolare liniara.
Modul in care se realizeazǎ interpolarea liniarǎ este dependentǎ de numǎrul de axe programabile ale masinii unelte cu comandǎ numericǎ.
In cazul in care sistemul de control al masinii este cu doua axe, interpolarea liniarǎ dupǎ o directie oarecare se realizeazǎ prin compunerea miscǎrilor pe cele douǎ axe, ponderea avansurilor pe cele douǎ directii fiind datǎ de orientarea deplasǎrii relativ la axe.(figura 4.91)
In cazul sistemelor programabile dupǎ trei axe existǎ doua posibilitǎti diferite:
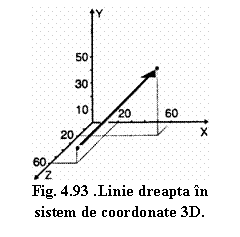
Programarea liniilor drepte numai in unul sau mai multe planuri fixe (Figura 4.92.). In acest caz scula executǎ miscare de avans transversal dupǎ directia Z iar pe celelalte dou axe are loc interpolarea liniara.
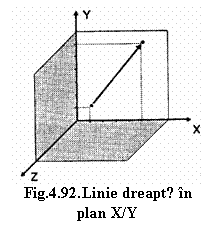
Programarea liniilor drepte oarecare "in spatiu"( Figura 4.93.) In acest caz, scula poate fi deplasata de-a lungul unei linii drepte de la un punct dat spre orice punct arbitrar in spatiu; interpolarea are loc pe toate cele trei axe.
In cazul unor sisteme de control, interpolarea liniara este posibila numai la anumite rapoarte bine definite intre cele douǎ axe de lucru.
Pozitionǎrile rapide se realizeazǎ cu avans rapid dar numai pe directiile axelor masinii.
INTERPOLAREA CIRCULARA
 Definirea unui cerc intr-un sistem de coordonate
bidimensional presupune cunoasterea
coordonatelor centrului acelui cerc si a razei acestuia (figura 4.94)
Definirea unui cerc intr-un sistem de coordonate
bidimensional presupune cunoasterea
coordonatelor centrului acelui cerc si a razei acestuia (figura 4.94)
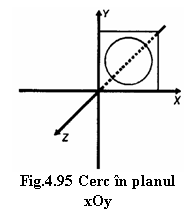
Pentru
definirea cercurilor intr-un sistem de coordonate tridimensional sunt necesare
specificarea planului in care se aflǎ cercul, coordonatele centrului
si raza acestuia 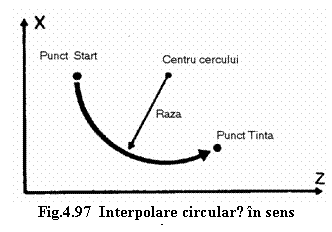 (Fig.4.95.)
(Fig.4.95.)
Deplasarea unei scule de la un punct de start spre un punct tinta de-a lungul unui traseu circular, se numeste interpolare circularǎ.
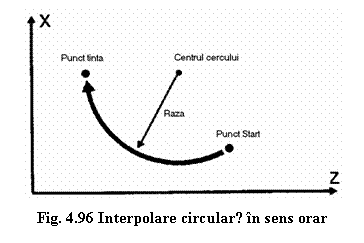
Interpolǎrile circulare se pot realiza prin deplasǎri circulare in sensul acelor de ceasornic (figura 4.96) sau in sens contrar acestora (figura 4.97).

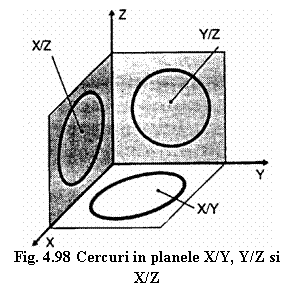 In cazul in care sistemul de control are mai mult de doua
axe controlabile NC, este necesarǎ precizarea planului
in care se realizeazǎ interpolarea circularǎ, adicǎ in planul
X/Y, X/Z sau Y/Z (figura 4.98)
In cazul in care sistemul de control are mai mult de doua
axe controlabile NC, este necesarǎ precizarea planului
in care se realizeazǎ interpolarea circularǎ, adicǎ in planul
X/Y, X/Z sau Y/Z (figura 4.98)
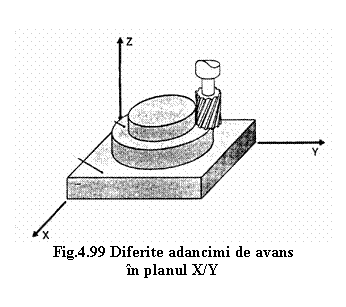
Dupǎ ce planul de definire al deplasǎrii circulare a fost ales se pot realiza prelucrǎri cu diferite adancimi de aschiere, acestea fiind programate dupǎ axa Z. In figura 4.99 sunt prezentate douǎ interpolǎri circulare in planul X/Y la diferite adancimi de aschiere.
In cazul interpolǎrilor circulare deplasǎrile rapide in mod normal nu sunt posibile.
RAZA SCULEI SI CORECTIA DE RAZA
Pentru realizarea prin frezare a unui contur dat, axa frezei trebuie sǎ urmeze o traiectorie astfel incat muchiile aschietoare ale acesteia sǎ urmeze conturul (Fig.4.100.).
Piesa frezata Traseu axa freza
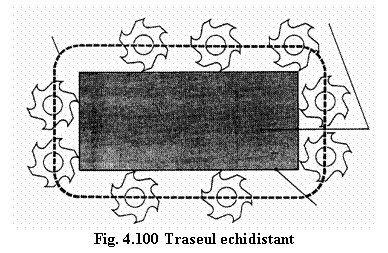 Traseul pe care-l
realizeazǎ axa frezei astfel incat sǎ realizeze conturul dat este
asa numitul "traseu echidistant".
Traseul pe care-l
realizeazǎ axa frezei astfel incat sǎ realizeze conturul dat este
asa numitul "traseu echidistant".
Contur piesa
In subcapitolelele anterioare s-au fǎcut
consideratii referitoare la deplasarile sculei, fara
insǎ a lua in calcul dimensiunile sculei si efectul acestora asupra
conturului sculei.
Fig. 2
Traseul frezei la atanga si la dreapta conturului finisat(prelucrat)
Pentru realizarea prin frezare a conturului piesei prezentate in fig.4.101, axa frezei trebuie sa se deplaseze de-a lungul traseului prezentat cu linie groasǎ.
Raza frezei Echidistanta Contur 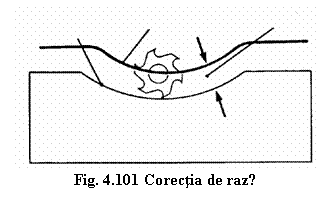
Acest
traseu al axei sculei este denumit "traseu echidistant ". Conturul real este
realizat prin rostogolirea unui cerc corespunzǎtor diametrului exterior al
frezei. Traiectoria centrului acestui cerc va fi la o distanta
datǎ in functie de raza sculei.
 La cele mai multe sisteme moderne
CNC, traseul echidistant este calculat in mod automat realizandu-se
corectia de razǎ implicit.
La cele mai multe sisteme moderne
CNC, traseul echidistant este calculat in mod automat realizandu-se
corectia de razǎ implicit.
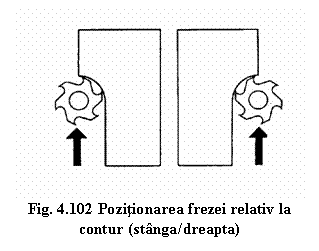
Realizarea corectiei de razǎ necesita introducerea prin program a urmatoarelor date :
dimensiunea razei frezei (fig. 4.101)
- pozitia frezei relativ la contur (pe stanga sau pe dreapta) considerand un sens dat de parcurgere al conturului. (fig. 4.102)
In general realizarea traseului echidistant este realizat de echipamentul de comandǎ numericǎ prin realizarea "calculǎrii punctelor suport".
Aceste
puncte sunt punctele de start si de sfarsit ale liniilor drepte
si ale arcelor de cerc, precum si ale centrelor cercurilor. Astfel
pentru realizarea coltului din figura 4.103. freza executǎ un arc de
cerc de razǎ egalǎ cu raza frezei si a cǎrui lungime este 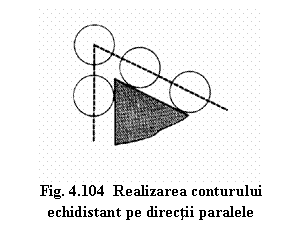
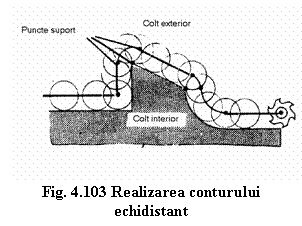 calculatǎ de echipamentul
de comandǎ numericǎ.
calculatǎ de echipamentul
de comandǎ numericǎ.
Existǎ echipamente de comandǎ numericǎ la care colturile se realizeazǎ doar prin deplasǎri strict paralele cu cele douǎ directii care formeazǎ coltul. (figura 4.104)
La prelucrǎrile pe comandǎ numericǎ prin strunjire, raza frezei este inlocuita de raza la varf a cutitului de strunjit (fig. 4.105).
In timpul programarii conturului, se presupune ca varful sculei este un punct ascutit care vine in contact cu conturul ce urmeazǎ a fi generat. Totusi, in realitate varful sculei este distantat, iar echipamentul de comandǎ numericǎ trebuie sa compenseze spatiul dintre varful teoretic al sculei si muchia aschietoare a sculei prin calcularea traseului echidistant adecvat.
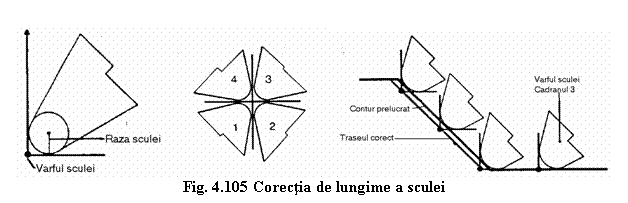 Pentru a ne asigura ca acest traseu echidistant este
intotdeauna atribuit partii corecte de contur, este necesara
introducerea "cadranului" adecvat in control (fig. 4.105) si aceasta
introducere determina directia din care varful sculei avanseaza
spre contur (fig.4.105)
Pentru a ne asigura ca acest traseu echidistant este
intotdeauna atribuit partii corecte de contur, este necesara
introducerea "cadranului" adecvat in control (fig. 4.105) si aceasta
introducere determina directia din care varful sculei avanseaza
spre contur (fig.4.105)
Traseele echidistante sunt obtinute prin "calculele punctelor suport". Aceste calcule determina toate punctele importante ce reprezinta traseele echidistante.
Pentru realizarea unei corectii corespunzǎtoare a lungimii sculei datele care trebuie transmise sistemului CNC sunt:
- raza la varf a cutitului de strunjit;
- pozitia cutitului (1,2,3,4) raportat la un cadran rectangular;
Aceastǎ pozitie determinǎ directia in care scula avanseazǎ pe contur.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |