
Reprezentarea numerelor binare in virgula fixa
Este cunoscut faptul ca, un numar X poate fi exprimat, intr-un sistem de numeratie cu baza (radix) r, prin intermediul unei functii polinomiale de forma:
![]() (1.1)
(1.1)
unde prin ![]() au fost notati
coeficientii, de fapt cifrele, a caror valoare este
restrictionata la gama
au fost notati
coeficientii, de fapt cifrele, a caror valoare este
restrictionata la gama ![]() .
.
Numarul X dat de (1.1), are n cifre in partea intreaga, respectiv m cifre in partea fractionara, fiecare dintre acestea
avand asociata o pondere (![]() ) a carei
valoare depinde, in mod strict, de pozitia cifrei in cadrul
numarului. Cifrele partii intregi sunt separate de cele
corespunzatoare partii fractionare prin virgula, iar
acelea situate la dreapta virgulei corespund partii intregi cu
ponderi crescatoare inspre partea stanga, incepand cu poderea (
) a carei
valoare depinde, in mod strict, de pozitia cifrei in cadrul
numarului. Cifrele partii intregi sunt separate de cele
corespunzatoare partii fractionare prin virgula, iar
acelea situate la dreapta virgulei corespund partii intregi cu
ponderi crescatoare inspre partea stanga, incepand cu poderea (![]() ) pentru cifra cea
mai putin semnificativa, respectiv cu ponderea (
) pentru cifra cea
mai putin semnificativa, respectiv cu ponderea (![]() ) pentru cifra cea
mai semnificativa. Tot asa, cifrele situate la dreapta virgulei
corespund partii fractionare a numarului si prezinta
ponderi descrescatoare incepand cu (
) pentru cifra cea
mai semnificativa. Tot asa, cifrele situate la dreapta virgulei
corespund partii fractionare a numarului si prezinta
ponderi descrescatoare incepand cu (![]() ), pentru cifra
situata imediat la dreapta virgulei, respectiv (
), pentru cifra
situata imediat la dreapta virgulei, respectiv (![]() ) pentru cifra
situata la distanta cea mai mare de virgula. Scrierea lui X in forma (1.1) justifica
atribuirea termenului de notatie pozitionala (positional
notation) a numarului.
) pentru cifra
situata la distanta cea mai mare de virgula. Scrierea lui X in forma (1.1) justifica
atribuirea termenului de notatie pozitionala (positional
notation) a numarului.
In particular,
daca r=10, aplicand (1.1), se obtine reprezentarea zecimala,
ordinara a lui X. Tot asa
daca r=2, se obtine reprezentarea binara a lui X, implicand doar cifrele binare ( 0
si 1). Este momentul sa facem precizarea ca (1.1) cu r=2, nu corespunde, de fapt,
reprezentarii unui numar binar in calculator si aceasta
pentru ca pozitia, in general, variabila a virgulei
revendica pentru specificarea acesteia una din cifrele binare (bits) care
altfel ar contribui la cresterea preciziei de reprezentare. Este
ratiunea pentru care, in scopul evitarii "sacrificarii"
preciziei de reprezentare, numerele din calculatoare sunt fie intregi (![]() ) fie fractionare (
) fie fractionare (![]() ).Pentru cele doua categorii de numere nu este
necesara specificarea pozitiei virgulei, aceasta fiind
considerata implicit fie la dreapta celui mai putin semnificativ bit
(least significant bit, lsb) atunci
cand avem de-a face cu numere intregi, fie la stanga celui mai semnificativ
(most significant bit, msb) sau intre
acesta si succesinul lui inspre dreapta atunci cand avem de-a face cu
numere fractionare, prima dintre situatii corespunzand numerelor
fractionare fara semn, iar cea de a doua numerelor fractionare
prevazute cu semn. Cu alte cuvinte, reprezentarea celor doua
categorii de numere se realizeaza, in notatie pozitionala,
admitand pozitia virgulei ca implicare fixa.
).Pentru cele doua categorii de numere nu este
necesara specificarea pozitiei virgulei, aceasta fiind
considerata implicit fie la dreapta celui mai putin semnificativ bit
(least significant bit, lsb) atunci
cand avem de-a face cu numere intregi, fie la stanga celui mai semnificativ
(most significant bit, msb) sau intre
acesta si succesinul lui inspre dreapta atunci cand avem de-a face cu
numere fractionare, prima dintre situatii corespunzand numerelor
fractionare fara semn, iar cea de a doua numerelor fractionare
prevazute cu semn. Cu alte cuvinte, reprezentarea celor doua
categorii de numere se realizeaza, in notatie pozitionala,
admitand pozitia virgulei ca implicare fixa.
In cazul in care ne
referim la numere cu semn, prin conventie, acestuia ii este alocat bitul cel
mai din stanga, msb, cu valoare 0
penru numere pozitive si 1 pentru numere negative, atat pentru intregi cat
si pentru fractii. Se obtine, in acest mod, prima forma de
reprezentare a numerelor in virgula fixa asa, numitul format sau
cod semn - marime (sign -
magnitude, SM). Conform acestuia numarul X se prezinta ca o secventa de, admitem, n biti
de forma ![]() in care xn-1 reprezinta semnul,
in conventia mentionata, iar xn-2
are alocata ponderea 2n-2 si care se imparte la 2 pentru
fiecare pozitie inspre dreapta ajungand sa fie 20 pentru x0 aceasta pentru numere
intregi si pentru numere fractionare, xn-2 are
alocata ponderea 2-1, aceasta fiind impartita la
2 pentru fiecare pozitie inspre dreapta ajungand sa fie 2-n+1
pentru x0. Uzitand de
cunoscuta identitate
in care xn-1 reprezinta semnul,
in conventia mentionata, iar xn-2
are alocata ponderea 2n-2 si care se imparte la 2 pentru
fiecare pozitie inspre dreapta ajungand sa fie 20 pentru x0 aceasta pentru numere
intregi si pentru numere fractionare, xn-2 are
alocata ponderea 2-1, aceasta fiind impartita la
2 pentru fiecare pozitie inspre dreapta ajungand sa fie 2-n+1
pentru x0. Uzitand de
cunoscuta identitate ![]() pentru numerele
intregi in SM rezulta domeniul valoric de reprezentare ca fiind 0 ≤
|X| ≤ 2n-1 -1, unde
prin |X| am notat valoarea
absoluta a lui X. Tot asa,
pentru numerele fractionare in SM rezulta domeniul valoric de reprezentare
ca fiind 0 ≤ |X| ≤ 1- 2n-1. .
pentru numerele
intregi in SM rezulta domeniul valoric de reprezentare ca fiind 0 ≤
|X| ≤ 2n-1 -1, unde
prin |X| am notat valoarea
absoluta a lui X. Tot asa,
pentru numerele fractionare in SM rezulta domeniul valoric de reprezentare
ca fiind 0 ≤ |X| ≤ 1- 2n-1. .
Referindu-ne la
precizia reprezentarii, avand cuvinte de n biti in SM putem
reprezenta ![]() numere binare fiecare
avand partea de marime specificate pe cel mult (n-1) biti. Corespunzator
acestora, raportandu-ne la mai familiarul sistem de numeratie cu r=10,
de transformarea bazei
logaritmice, cifrele numerelor zecimale pot fi cel mult
numere binare fiecare
avand partea de marime specificate pe cel mult (n-1) biti. Corespunzator
acestora, raportandu-ne la mai familiarul sistem de numeratie cu r=10,
de transformarea bazei
logaritmice, cifrele numerelor zecimale pot fi cel mult ![]() , unde barele
, unde barele ![]() semnifica cel mai
mic intreg mai mare decat valoarea calculata pentru expresia dintre bare.
semnifica cel mai
mic intreg mai mare decat valoarea calculata pentru expresia dintre bare.
Reprezentare SM a
numerelor binare prezinta avantaje constand din simplitate conceptual,
domeniu valoric simetric, negare simpla prin inversarea bitului de semn,
precum si un cost redus al implementarilor care apeleaza la
acest format, cum va rezulta, spre exemplu, la sinteza dispozitivelor de
inmultire. Totusi, codul SM prezinta doua dezavantaje
importante, dintre care primul vizeaza operatia de adunare. Ori este
stiut, aceasta este foarte solicitata intrucat majoritatea
algoritmilor pentru operatii de complexitate superioara se reduce, in
ultima instanta, la adunare. Pe de alta parte, unul dintre
principiile fundamentale ale proiectarii calculatoarelor statueaza ca,
pentru a obtine performante relativ la accelerarea calculelor, se
impune favorizarea prin solutii tehnice a acelor parti din
sistem care sunt mai solicitate ("Make the common case fast") [HePa 03]. 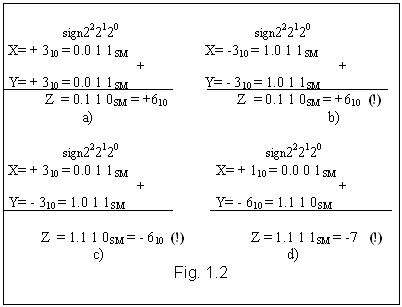 Evaluarea cantitativa a
accelerarii realizate prin aplicarea acestui principiu se obtine prin
asa numita lege a lui Amdahl, ori, in baza acesteia, operatia de
adunare se impune favorizata in sensul gasirii acelor solutii
care sa permita implementarea ei cat mai facila, implicit cat
mai performanta. Dar adunarea in SM pune probleme in sensul ca
difera realizarea acesteia in situatia ca operanzii au
acelasi semn, fata de cea cand acestia prezinta semne
diferite. Astfel, considerand n = 4 si numere intregi, in fig. 1.2 a se prezinta cazul in care operanzii sunt
amandoi pozitivi si exista suficienti biti pentru
reprezentarea rezultatului (este evitata situatia speciala
asa numita de depasire), cand, se poate observa, rezultatul
suma este obtinut in mod corect. O prima problema apare atunci
cand operanzii au acelasi semn, fiind amandoi negativi (fig. 1.2 b). Chiar
daca insumarea partilor de marime se realizeaza
corect, bitul de semn nu poate fi tratat ca un bit ordinar, el necesitand a fi
setat in mod separat pe baza prealabilitationari a bitilor
de semn ai operanzilor. Tot cu o tatonare a semnelor celor doi operanzi trebuie
sa se efectueze si adunarile exemplu din fig. 1.2 c si fig.
1.2 d. In aceste cazuri, cand semnele operanzilor difera, adunarea trebuie
substituita prin scadere, care trebuie precedata de compararea
partilor de marime ale operanzilor. Pentru a evita aparitia
unor rezultate eronate la adunarea numerelor in SM, se impune suplimentarea
structurii dispozitivului de insumare cu un comparator de marime, o
schema separata de scadere precum si solutii pentru
tatonarea semnelor operatiilor, ceea ce determina nu numai o
suplimentare a investitiei, ci si degradarea performantei
executiei operatiei, acest din urma aspect mai important, prin prisma
legii lui Amdahl, decat primul. Exista si modalitatea de solutionare
bazata, anticipam, pe precomplementare si postcomplementare
selectiva [Park00], dar si aceasta apeleaza la circuite si
intarzieri suplimentare.
Evaluarea cantitativa a
accelerarii realizate prin aplicarea acestui principiu se obtine prin
asa numita lege a lui Amdahl, ori, in baza acesteia, operatia de
adunare se impune favorizata in sensul gasirii acelor solutii
care sa permita implementarea ei cat mai facila, implicit cat
mai performanta. Dar adunarea in SM pune probleme in sensul ca
difera realizarea acesteia in situatia ca operanzii au
acelasi semn, fata de cea cand acestia prezinta semne
diferite. Astfel, considerand n = 4 si numere intregi, in fig. 1.2 a se prezinta cazul in care operanzii sunt
amandoi pozitivi si exista suficienti biti pentru
reprezentarea rezultatului (este evitata situatia speciala
asa numita de depasire), cand, se poate observa, rezultatul
suma este obtinut in mod corect. O prima problema apare atunci
cand operanzii au acelasi semn, fiind amandoi negativi (fig. 1.2 b). Chiar
daca insumarea partilor de marime se realizeaza
corect, bitul de semn nu poate fi tratat ca un bit ordinar, el necesitand a fi
setat in mod separat pe baza prealabilitationari a bitilor
de semn ai operanzilor. Tot cu o tatonare a semnelor celor doi operanzi trebuie
sa se efectueze si adunarile exemplu din fig. 1.2 c si fig.
1.2 d. In aceste cazuri, cand semnele operanzilor difera, adunarea trebuie
substituita prin scadere, care trebuie precedata de compararea
partilor de marime ale operanzilor. Pentru a evita aparitia
unor rezultate eronate la adunarea numerelor in SM, se impune suplimentarea
structurii dispozitivului de insumare cu un comparator de marime, o
schema separata de scadere precum si solutii pentru
tatonarea semnelor operatiilor, ceea ce determina nu numai o
suplimentare a investitiei, ci si degradarea performantei
executiei operatiei, acest din urma aspect mai important, prin prisma
legii lui Amdahl, decat primul. Exista si modalitatea de solutionare
bazata, anticipam, pe precomplementare si postcomplementare
selectiva [Park00], dar si aceasta apeleaza la circuite si
intarzieri suplimentare.
Dezavantajul lui constand din dificultatile relevate la operatia adunare i se mai adauga unul constand din faptul ca, in SM, exista doua reprezentari pentru .0 ((+) 0, adica 0.0.00 si (-)0, adica 1.0..00). cum testarea faptului ca un rezultat este egal cu 0, implicat in, uzual, frecventele comparatii, este, de asemenea, o operatie solicitata s-ar impune solutionarea ei cat mai simpla, ceea ce ar reclama o singura reprezentare pentru 0 (ceea ce nu este posibil intr-un sistem binar cu domeniu valoric simetric).
In cautarea de solutii pentru surmontarea deficientelor expuse ale formatului SM, introducem, mai intai, formatul sau codul complement de unu (one's complement, C1). Acest format, utilizat in unele calculatoare mai vechi din epoca sistemelor de capacitate medie si mare (mainframe), isi pastreaza importanta prin contributia sa la forma reprezentarii in complement de doi (two's complement), care constituie competitorul real pentru codul SM.
In ceea ce priveste reprezentarea in C1 a unui numar X pe n biti, aceasta se noteaza cu X si este data de:
![]() ≥ 0.
≥ 0. ![]()
![]() X (1.2)
X (1.2)
≤ 1. ![]()
unde xi = 1- xi
Conform cu (1.2), numerele pozitive au in C1 o reprezentare identica cu cea din SM, iar pentru numerele negative din C1 se substituie fiecare cifra binara din formatul SM cu complementul de unu al respectivei cifre. Cum relatia aritmetica xi = 1- xi este echivalenta, fiind excluse perechile, (xi , xi) = (0,0) si (1,1), cu operatia logica xi = 1+ xi in care + reprezinta operatorul EXCLUSIVE-OR sau suma modulo 2. in consecinta poate fi format in mod simplu plecand de la forma in SM, trecand aceasi reprezentare printr-un nivel de porti EXCLUSIVE-OR, cate o poarta pentru fiecare bit a lui X, toate portile avand una dintre intrari comuna, la care se aplica un 0 (fara efect in termeni EXCLUSIVE-OR) atunci cand X > 0, respectiv un 1 (cu efect de complementare) atunci cand X < 0.
Cu caracteristicile
domeniu valoric si precizie asemanatoare formatului SM, facem
importanta mentiune numerelor negative din C1 nu le corespunde o
notatie pozitionala specifica unui cod ponderat. Analizand
comportamentul formatului C1 in raport cu deficientele semnalate la
reprezentarea in SM, prin prisma adunarii a doua numere pozitive, nu
exista deosebiri (vezi si fig. 1.2 a). Admitand in calitate de
exemplu, din nou, n = 4 si numere intregi, in fig. 1.3 se prezinta
situatii semnificative care pot sa apara la adunarea sumelor
reprezentate in C1. Astfel cazul din fig. 1.3 a corespunde adunarii a
doua numere de semne contrare si numarul negativ este, in
valoare absoluta, mai mare sau egal cu cel pozitiv. Se observa o
efectuarea corecta a operatiei si explicatia rezida in
faptul ca, admitand |Y| ≥
X, la partea de marime a lui X se va aduna un numar care,
tinand cont de (1.2), prezinta cel mult valoarea complementata
de unu a lui X. In
consecinta, in conditiile specificate, nu poate exista transport
inspre bitul de semn, deci acesta ramane 1, rezultatul suma fiind
negativ. Pe de alta parte![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , atunci cand se aduna doua
numere de semne contrare , dar de aceasta data, numarul pozitiv
este, in valoare absoluta, mai mare decat cel negativ (fig. 1.3 b) sau
cind se aduna doua numere negative (fig. 1.3 c) rezultatul se
obtine in urma aplicarii unei corectii constand din adunarea la
bitul lsb al sumei a tranportului din
bitul de semn (end-around carry).
, atunci cand se aduna doua
numere de semne contrare , dar de aceasta data, numarul pozitiv
este, in valoare absoluta, mai mare decat cel negativ (fig. 1.3 b) sau
cind se aduna doua numere negative (fig. 1.3 c) rezultatul se
obtine in urma aplicarii unei corectii constand din adunarea la
bitul lsb al sumei a tranportului din
bitul de semn (end-around carry).
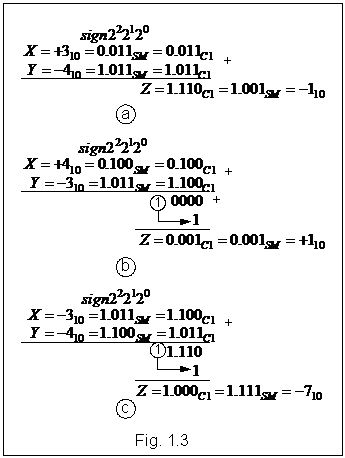 Referindu-ne la cazul din fig. 1.3 b,
cand, in SM, |Y| < X, si apeland la rationamentul
, mai degraba intuitiv, uitat si anterior, constatam ca la
partea de marime a lui X se
aduna o valoare mai mare, la limita egala, care, tinand
cont de (1.2), va determina un transport inspre bitul semn. Acesta se va aduna
la valoarea 1 obtinuta ca suma a bitilor de semn (x>0, y<0), astfel incat va rezulta
un transport din bitul de semn, aceasta din urma devenind 0,
corespunzator unui rezultat pozitiv. In aceste conditii,
operatia de adunare se reduce la o scadere cu descazutul mai
mare decat scazatorul, iar influenta adunarii combinatiei
11.11, prevazuta de (1.2), trebuie eliminata ceea ce se
intampla intr-adevar atunci cand se aduna transportul generat
din adunarea bitilor de semn la bitul lsb
al sumei intermediare (end-around carry). Mai atentionam ca
printr-un rationament simplificat, asemanator celui de mai sus,
poate fi justificat si cazul particularizat in fig. 1.3 c.
Referindu-ne la cazul din fig. 1.3 b,
cand, in SM, |Y| < X, si apeland la rationamentul
, mai degraba intuitiv, uitat si anterior, constatam ca la
partea de marime a lui X se
aduna o valoare mai mare, la limita egala, care, tinand
cont de (1.2), va determina un transport inspre bitul semn. Acesta se va aduna
la valoarea 1 obtinuta ca suma a bitilor de semn (x>0, y<0), astfel incat va rezulta
un transport din bitul de semn, aceasta din urma devenind 0,
corespunzator unui rezultat pozitiv. In aceste conditii,
operatia de adunare se reduce la o scadere cu descazutul mai
mare decat scazatorul, iar influenta adunarii combinatiei
11.11, prevazuta de (1.2), trebuie eliminata ceea ce se
intampla intr-adevar atunci cand se aduna transportul generat
din adunarea bitilor de semn la bitul lsb
al sumei intermediare (end-around carry). Mai atentionam ca
printr-un rationament simplificat, asemanator celui de mai sus,
poate fi justificat si cazul particularizat in fig. 1.3 c.
Referindu-ne la cel de-al doilea dezavantaj semnalat la reprezentarea in SM, cel constand in testarea " de 0", se poate remarca faptul ca si formatul C1prezinta acest neajuns, operatia necesitand compararea cu doua valori, in loc de una singura, si anume cu 0.000. pentru (+) 0, respectiv cu 1.111, pentru (-) 0.
Dar ambele deficiente majore relevate la formatul SM, si pastrate si la reprezentarea in C1, sunt inlaturate daca se apeleaza la formatul sau codul complement de doi (two's complement, C2). Referindu-ne mai intai, la modul de formare a acestuia, pentru un numar X pe n biti, de tip intreg, notand cu (-X) reprezentarea in C2, avem:
![]() ≥ 0. xn-2
xi. x1 x0
≥ 0. xn-2
xi. x1 x0
![]() - X =
- X =
≤ (1. xn-2 xi. x1 x0 + 1) mod 2n
unde prin mod 2n am notat suma care se efectueaza modulo 2n.
Tot asa, daca numarul X pe n biti este de tip fractionar, atunci complementul sau de doi este data de:
![]() ≥ 0. xn-2 xi. x1
x0
≥ 0. xn-2 xi. x1
x0
![]() - X =
- X =
≤ (1. xn-2 xi. x1 x0 + 0.0.0.01) mod 2n
unde, din nou, prin mod 2 am notat suma care se efectueaza modulo 2.
 Dupa cum rezulta din (1.3)
si (1.4), reprezentarea numerelor pozitive este identica cu cea din
SM si C1. Pentru numerele negative, se formeaza, mai intai, reprezentare
in C1,iar apoi, la pozitia lsb a
acesteia se aduna o unitate binara. La acesta din urma
opratie se ignora eventualul transport din pozitia msb, cea corespunzatoare
bitilor de semn, fie specificat in (1.3) si (1.4), prin efectuarea
sumelor modulo 2n, respectiv modulo 2. Mentionam ca
exista si o regula practica de formare a C2 conform
careia se pleaca de la reprezenarea in SM si se parcurge aceasta
de la dreapta inspre stanga pastrand toti bitii precum si
primul bit de 1 intalnit, dupa care se substituie restul de biti prin
valorile lor complementare (de unu), adica toti bitii de 0 devin
1, asa cum toti biti de 1 devin 0.
Dupa cum rezulta din (1.3)
si (1.4), reprezentarea numerelor pozitive este identica cu cea din
SM si C1. Pentru numerele negative, se formeaza, mai intai, reprezentare
in C1,iar apoi, la pozitia lsb a
acesteia se aduna o unitate binara. La acesta din urma
opratie se ignora eventualul transport din pozitia msb, cea corespunzatoare
bitilor de semn, fie specificat in (1.3) si (1.4), prin efectuarea
sumelor modulo 2n, respectiv modulo 2. Mentionam ca
exista si o regula practica de formare a C2 conform
careia se pleaca de la reprezenarea in SM si se parcurge aceasta
de la dreapta inspre stanga pastrand toti bitii precum si
primul bit de 1 intalnit, dupa care se substituie restul de biti prin
valorile lor complementare (de unu), adica toti bitii de 0 devin
1, asa cum toti biti de 1 devin 0.
Din descrierea realizata pentru formarea C2, rezulta ca la stratul de circuite EXCLUSIVE - OR, care permit generarea C1, se adauga un dispozitiv de insumare care sa permita adunarea unui 1 la lsb-uri complementului de unu. Se poate conchide ca formarea C2 este mai complicata decat a celorlalte doua reprezentari, SM si C1, ceea ce constituie un dezavantaj. Tot la acest capitol poate fi incadrat si faptul ca, pentru numere negative, C2 nu reprezinta un cod ponderat in confirmitate cu notatia pozitionala.
Dar aceste aspecte devaforabile complementului de doi sunt contrabalansate prin facilitarea rezolvarii problemelor adunarii si testarii de 0, justificand competitia existenta intre C2 si SM, la implementare diferitelor proceduri care vizeaza numerele. Astfel, in cea ce priveste adunarea, uzitand de acelasi rationamente intuitive folosit la C1, se poate constata ca efectul end-around carry este peluat in mod anticipativ, de unitatea binara adunata la formarea C2. De asemenea, pentru cazul cand nu se genereaza end-around carry, unitatea binara adunata pentru formarea C2 face sa dispara efectul adunarii combinatiei 1111, implicata de (1.2), si, prin aceasta, rezultatul ramane nealterat. In consecinta, bitul de semn poate fi tratat ca oricare alt bit, ordinar, al numarului, facand necesara dispozitivele de testare a semnul, de comparare a marimilor si de scadere sau pre- si post complementare selectiva, revendicate de executie corecta a operatiei de adunare in SM. In figura 1.4 sunt reluate exemplele din fig. 1.3, fiind executate, de aceasta data in C2.
Consecinta a modului de operare in C2este faptul ca scaderea se reduce la adunare, constand din insumare la numarul descazut (minuend) a complementului de doi corespunzator scazatorului (subtrahend), este posibila, deci, implementarea celor doua operatii fundamentale, la care se pot reduce cele mai complexe, printr-unul si acelasi dispozitiv, corespunzator comandat. Privita aceasta problematica prin prisma legii lui Andahl, reprezentarea in C2 se prezinta ca favorabila celor doua reprezentari de virgula fixa, SM si C1.
Referindu-ne la
testarea de 0, se poate remarca in mod facil ca modul de formare a
complementului doi determina o reprezentare unica pentru 0,
facand necesara o singura comparatie. In fig. 1.5,
acceptand deja folositul n = 4, sunt
date comparativ codurile binare de virgula fixa (fixed-point binary
codes) pentru unele dintre numerele zecimale (decimal number) intregi. 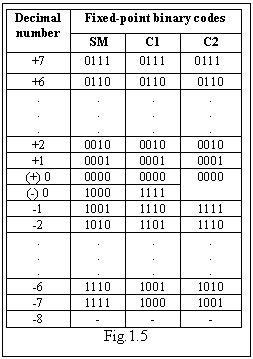 Este
de remarcat ca unica reprezentare pentru 0 in C2 face sa
ramana disponibila combinatia de 1 urmat, la dreapta, de
0-uri, numar a carui cod in C2 este el insusi. Aceasta
asimetrie a domeniului valoric cunoscuta si ca anomalie a
complementului de doi reperezinta un oarecare dezavantaj fata de
celelate doua coduri, ambele simetrice.
Este
de remarcat ca unica reprezentare pentru 0 in C2 face sa
ramana disponibila combinatia de 1 urmat, la dreapta, de
0-uri, numar a carui cod in C2 este el insusi. Aceasta
asimetrie a domeniului valoric cunoscuta si ca anomalie a
complementului de doi reperezinta un oarecare dezavantaj fata de
celelate doua coduri, ambele simetrice.
In continuare, ne vom referii global la formatele de virgula fixa remarcand ca, datoria disponibilitatii pentru reprezentare a unui numar (n) limitat de biti, valorile pot fi afectate de erori. Astfel, in mod frecvent, o operatie implicand numere pe n biti produce un rezultat pe mai mult de n biti. In acelasi sens, daca, spre exemplu, inmultim doi operanzi pe n biti, pentru produs ar putea fi necesari 2*n biti, ori, fiind disponibili doar n pentru reprezentare, rezultatul operatiei va fi afectat de o eroare. Aceasta ar putea fi obtinuta prin urmare a completei omiteri a unor biti, cum ar fi cei mai putin semnificativi n biti ai produsului de 2*n biti. Procedand astfel, se obtine o asa numita eroare de trunchiere (truncation error). Efectul acestei categorii de erori prin omitere poate fi diminuat apeland insa la o operatie suplimentara, numita rotunjire (rounding) - descrisa amanuntit in ultimul capitol, prin care eroarea devine de rotunjire (roundoff error). Realizand calcule succesive, potential afectate de erori de trunchiere sau rotunjire, se poate ajunge la un cumul al acestora care poate sa fie intorelabil. In consecinta, alegerea formatelor de virgula fixa pentru reprezentarea numerelor trebuie realizata astfel incat sa aiba suficienta precizie sau, in unle cazuri, se impune efectuarea calculelor cu grad de precizie sporit, cand, pentru anumite rezultate se tolereaza reprezentarea pe mai multe cuvinte in asa numita aritmetica de precizie multipla (multiple precision).
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |