Cazuri exceptate la calculul limitelor de siruri

Cazuri exceptate la calculul limitelor de siruri

In cele ce urmeaza se presupun cunoscute :

Propozitia 1

a) Pentru orice sirul este convergent si .

b) Pentru orice avem .

Propozitia 2

a) Pentru orice sirul este convergent si .

b) Pentru orice sirul are limita egala cu .

1.1 Cazul

Daca si sunt doua siruri astfel incat si , sau invers, atunci nu se poate preciza ce limita are sirul si nici daca are limita. Justificam aceasta afirmatie prin exemplele care urmeaza.

Exemplul 1. Fie si date prin . Atunci avem si . Dar deci .

Exemplul 2. Fie si date prin. Atunci avem si . Dar . Deci .

Exemplul 3. Fie si date prin . Atunci avem si . Dar . Deci .

Exemplul 4. Fie si date prin unde este arbitrar ales. Atunci avem si . Dar si prin urmare avem :

.

Exemplul 5. Fie si date prin . Pentru ca si avem si evident . Pe de alta parte , ceea ce demonstreaza ca sirul nu are limita.

Din exemplele de mai sus deducem ca daca si sau invers, atunci sirul poate sa aiba limita 0 sau sau sau orice numar real sau poate sa nu aiba limita.

1.2 Cazul

Daca si sunt doua siruri astfel incat si , sau invers, atunci nu se poate preciza ce limita are sirul si nici daca are limita. Justificam aceasta afirmatie prin exemplele care urmeaza.

Exemplul 1 Fie si date prin . Atunci: , , si .

Exemplul 2 Fie si date prin . Atunci: , , si .

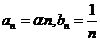Exemplul 3 Fie arbitrar ales si , date prin . Atunci , , si .

Exemplul 4 Fie si date prin . Atunci . Pe de alta parte din deducem . Dar , ceea ce arata ca sirul nu are limita.

1.3 Cazul

Daca si sunt doua siruri astfel incat si atunci nu se poate preciza ce limita are sirul 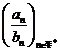si nici daca are limita, dupa cum rezulta din exem­plele care urmeaza.

Exemplul 1 Fie si date prin . Atunci ,, .

Exemplul 2 Fie si date prin . Atunci ,, .

Exemplul 3 Fie si date prin . Atunci , , .

Exemplul 4 Fie si date prin . Deoarece avem si , deducem ca . Evident si , ceea ce arata ca 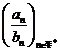nu are limita.

1.4 Cazul

Daca si sunt doua siruri astfel incat si atunci nu se poate preciza ce limita are sirul 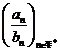si nici daca are limita, dupa cum rezulta din exem­plele care urmeaza.

Exemplul 1 Fie si date prin . Atunci si .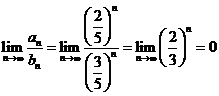

Exemplul 2 Fie si date prin . Atunci si .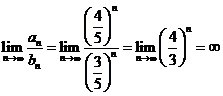

Exemplul 3 Fie si date prin . Atunci si .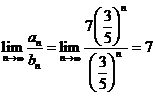

Exemplul 4 Fie si date prin . Atunci si , ceea ce arata ca 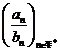nu are limita.

1.5 Cazurile , ,

Pentru a justifica de ce aceste operatii sunt exceptate observam ca daca si sunt doua siruri astfel incat atunci . Aceasta relatie arata ca pentru a evalua limita sirului trebuie sa evaluam limita sirului , ceea ce ne conduce la unul dintre cazurile de mai sus. Avem in vedere ca: ; si .