
Frecventa relativa si probabilitatea frecventei relative in cursul unor masuratori (incercari - probe) repetate.
Sa ne imaginam ca se efectueaza o serie de n probe. In cursul fiecarei probe un eveniment A poate sa aiba loc cu probabilitatea p. Fie x variabila aleatoare ce defineste frecventa relativa de realizare a evenimentului A in cursul unei serii de n probe. Se cere sa se determine legea de distributie a variabilei aleatoare x pentru o serie de n probe.
Este evident ca variabila aleatoare n va lua in cursul celor n probe una din valorile urmatoare:
![]() ,
, ![]() , .. ,
, .. , ![]()
Teorema 1: Probabilitatea P(x = ![]() ) pentru ca variabila aleatoare x sa
ia valoarea
) pentru ca variabila aleatoare x sa
ia valoarea ![]() , altfel spus, pentru ca in cursul a n probe,
evenimentul A sa se realizeze de m ori si
evenimentul contra
, altfel spus, pentru ca in cursul a n probe,
evenimentul A sa se realizeze de m ori si
evenimentul contra ![]() (A nu
are) de (n-m) ori este
egala
(A nu
are) de (n-m) ori este
egala ![]() unde
unde ![]() este numarul de
combinatii de n elemente luate de m ori; p este probabilitatea
evenimentului A; p = P(A); q este probabilitatea de nerealizare a
evenimentului A, altfel spus q = 1- p = P(
este numarul de
combinatii de n elemente luate de m ori; p este probabilitatea
evenimentului A; p = P(A); q este probabilitatea de nerealizare a
evenimentului A, altfel spus q = 1- p = P(![]() ) .
) .
Demonstratie: Evenimentul A
se produce de m ori in cursul a n probe daca
de exemplu, evenimentele ![]() si A
se succed dupa cum urmeaza:
si A
se succed dupa cum urmeaza:
![]()
![]() AA.........A
AA.........A ![]()
![]() ....
....![]()
n n-m
Altfel spus, in cursul primelor m probe, evenimentul A apare si in cursul ultimului (n-m)
urmatoare probe, evenimentul nu apare adica se realizeaza
evenimentul (![]() ).
).
Dar conform teoremei:
P(A)
= p P(![]() ) = 1- p = q
) = 1- p = q
In virtutea termenului produsului, probabilitatea unei astfel de succesiuni de evenimente va fi:
pm qn - m
Evenimentul A poate de
asemenea sa se produca de m ori in cursul celor n
probe cu o alta succesiune a evenimentelor A si ![]() , de exemplu urmatoarea succesiune:
, de exemplu urmatoarea succesiune:
![]() AA.........A
AA.........A ![]()
![]() ....
....![]() A
A
![]()
![]() m-1 n-m 1
m-1 n-m 1
Necesar este ca evenimentul A sa se produca cu necesitate de m ori si evenimentul A de n-m ori. Probabilitatea unei astfel de succesiuni este:
Pm-1 qn-m p = pm q n - m
Dar cate succesiuni diferite ale
evenimentelor A si ![]() sunt posibile pentru n
probe daca evenimentul A este realizat de m
ori.
sunt posibile pentru n
probe daca evenimentul A este realizat de m
ori.
Este evident ca numarul lor corespunde numarul de combinatii de n elemente luate de m ori.
![]() =
= ![]()
Vom obtine, conform teoremei ca:
![]() P( x =
P( x =![]() ) = pm q n
- m + pm q n - m + ..+ pm q n - m
) = pm q n
- m + pm q n - m + ..+ pm q n - m
![]()
sau inca:
P( x =![]() ) =
) = ![]() pm q n
- m (VII 27)
pm q n
- m (VII 27)
si teorema este demonstrata.
Demonstratia teoremei ne permite sa definim legea de distributie a unei variabile aleatoare x, pe care o punem sub forma de tablou:
![]()
![]()
x ![]()
![]()
![]() ... .
... . ![]() .
. ![]()
![]()
![]() P( x =
P( x =![]() ) 1* qn
) 1* qn ![]() pq n - 1
pq n - 1 ![]() p2q n - 2
p2q n - 2 ![]() pmqn - m ..
pmqn - m .. ![]()
Legea de distributie astfel obtinuta se numeste lege binomiala deoarece probabilitatea :
P( x =![]() )
)
sunt egali cu termenii corespunzatori dezvoltarii expresiei:
(q + p)n
dupa formula binomiala:
(q + p)m = ![]() (VII 28)
(VII 28)
suma probabilitatilor tuturor valorilor posibile este dupa cum se poate vedea egala cu 1, deoarece:
(p + q)m = 1n =1
Remarca: In studiul diferitelor probleme avem nevoie de
a determina probabilitatea pentru ca evenimentul A sa fie
realizat cel putin o singura data, astfel spus frecventa
relativa a evenimentului x ![]() .
.
Este evident ca probabilitatea P(
x ![]() ) este determinata plecand de la
egalitatea:
) este determinata plecand de la
egalitatea:
P( x ![]() ) = 1 - p( x =
) = 1 - p( x = ![]() ) = 1- qn (VII 29)
) = 1- qn (VII 29)
Din tabloul de
distributie rezulta ca probabilitatea P(
x ![]() ), pentru ca evenimentul sa aiba loc de cel
putin k ori va fi determinat de formula:
), pentru ca evenimentul sa aiba loc de cel
putin k ori va fi determinat de formula:
P( x ![]() ) =
) = ![]() (VII 30)
(VII 30)
sau inca:
P( x ![]() ) = 1 -
) = 1 - ![]() (VII
31)
(VII
31)
Exemplul 1: Sa se reprezinte
grafic legea de distributie a unei variabile aleatoare x
pentru n = 8, p ![]() ; q =
; q = ![]()
Solutie: Determinam toate valorile probabilitatilor din tablou:
P( x=0) = ![]() = 1
= 1 ![]() =
= ![]()
P( x=![]() ) =
) = ![]()
![]() (
(![]() )7 =
)7 = ![]()
![]() =
= ![]()
P( x=![]() ) =
) = ![]() (
(![]() )8 =
)8 = ![]()
![]() =
= ![]()
P( x=![]() ) =
) = ![]() (
(![]() )8 =
)8 = ![]()
![]() =
= ![]()
P( x=![]() ) =
) = ![]() (
(![]() )8 =
)8 = ![]()
![]() =
= ![]()
P( x=![]() ) =
) = ![]() (
(![]() )8 =
)8 = ![]()
P( x=![]() ) =
) = ![]() (
(![]() )8 =
)8 = ![]()
P( x=![]() ) =
) = ![]() (
(![]() )8 =
)8 = ![]()
P( x=![]() ) =
) = ![]() (
(![]() )8 =
)8 = ![]()
Graficul acestei reprezentari este:
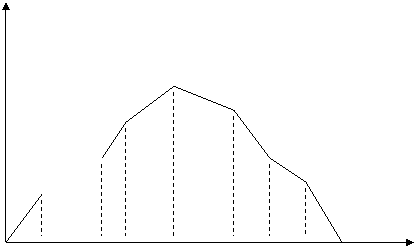
p
![]()
![]()
O ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Exemplul 2: Care este probabilitatea pentru ca evenimentul A sa se produca de 2 ori:
a) in timpul a doua probe
b in cursul a trei probe
c) in cursul a zece probe daca probabilitatea de realizare are un eveniment in cursul fiecarei probe de 0,4.?
Solutie:
a) Aici n=2; p=0,4 ; q=0,6
P( x = ![]() ) =
) = ![]() =
= ![]() = 0,16
= 0,16
b) Aici n=3; p=0,4 ; q=0,6
P( x = ![]() ) =
) = ![]() =
= ![]() * 0,6 = 0,288
* 0,6 = 0,288
c) Aici n=10; p=0,4 ; q=0,6
P( x = ![]() ) =
) = ![]() =
= ![]() (0,6)8 = 0,121
(0,6)8 = 0,121
Exemplul 3: Se efectueaza 4 probe independente. Probabilitatea de realizare a evenimentului A este 0 pentru fiecare proba. Sa se determine probabilitatea pentru ca evenimentul A sa se realizeze de cel putin 2 ori.
Solutie: Aici n = 4; p = 0,5 ; q = 0,5;
P(x ![]()
![]() ) = P(x =
) = P(x =![]() ) + P(x =
) + P(x =![]() ) + P(x =
) + P(x =![]() )
)
sau
P(x ![]()
![]() ) = 1 - P(x =
) = 1 - P(x =![]() ) + P(x =
) + P(x =![]() )
)
Calculam probabilitatea:
P(x <![]() ) = P(x
=
) = P(x
=![]() ) + P(x =
) + P(x =![]() ) = q4 + 4q3 p1 = (0,5)4
+ 4(0,5)4 = 0,3125
) = q4 + 4q3 p1 = (0,5)4
+ 4(0,5)4 = 0,3125
Vom obtine in consecinta utilizand formula a doua:
P(x ![]()
![]() ) = 1 - [(0,5)4 + 4(0,5)4] = 0,6875
) = 1 - [(0,5)4 + 4(0,5)4] = 0,6875
Exemplul 4: Probabilitatea rebutului intr-un lot de piese este p = 0 . Care este probabilitatea pentru ca intr-un lot de 3 piese sa avem m = 0; m = 1; m = 2; m = 3 piese defecte?
P( x =![]() ) =
) = ![]() = 1 (0,9)3 = 0,729
= 1 (0,9)3 = 0,729
P( x =![]() ) =
) = ![]() p2 q =
p2 q =
![]()
![]() = 0,243
= 0,243
P( x =![]() ) =
) = ![]() p q2 =
p q2 = ![]() .
.![]() . (0 )2 * (0,9) = 0,027
. (0 )2 * (0,9) = 0,027
P( x =![]() ) =
) = ![]() p3 = 1.(0,1)3
= 0,001
p3 = 1.(0,1)3
= 0,001
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |