
PROBLEME DE EXTREM IN GEOMETRIE SI FIZICA
Analiza matematica este deosebit de utila si la orele de fizica si matematica. Este deosebita o ora de matematica si fizica, cu profesorii de ambele specialitati: cel de fizica expune fenomenul fizic , iar cel de matematica ofera suporutl matematic. Copiilor le place deosebit. Incercati. . .
PROBLEMA 1. In triunghiul isoscel ABC cu baza BC=2a si inaltimea AD=h, sa se inscrie dreptunghiul de arie maxima, cu o latura pe baza BC.
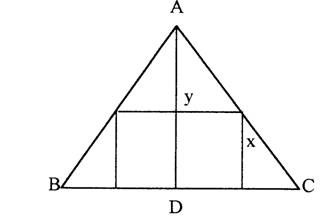
Solutie. Vom nota cu x si y laturile dreptunghiului . Din asemanarea triunghiurilor avem relatia:
![]() Þ y=
Þ y=![]()
Þ S(x)= yx = ![]() unde S(x) am notat aria dreptunghiului.
unde S(x) am notat aria dreptunghiului.
Deci, S(x)= ![]() Þ S(x) =
Þ S(x) =![]() +ax Þ S¢(x)=
+ax Þ S¢(x)=![]() +a
+a
S¢(x)=0 Þ ![]() +a =0 Þ -2ax= -ah Þ x=
+a =0 Þ -2ax= -ah Þ x=![]()
Studiind semnul lui S¢(x) :
|
x |
|
|
S¢(x) |
+ + + + + + + 0 - - - - - - - - - - - |
|
S(x) |
|
Þ x=![]() punct de maxim local Þ Smax=S(
punct de maxim local Þ Smax=S(![]() )=
)=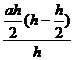 Þ Smax=
Þ Smax=![]() Þ Smax =
Þ Smax = ![]() .
.
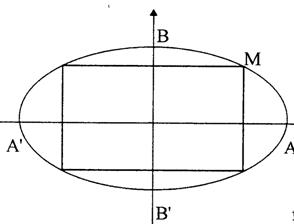
PROBLEMA 2. Sa se inscrie in elipsa : ![]() , un dreptunghi
de arie maxima , avand laturile paralele cu axele elipsei.
, un dreptunghi
de arie maxima , avand laturile paralele cu axele elipsei.
Solutie. Fie MÎ elipsei Þ M are coordonatele (x, ![]() ).
).
Aria dreptunghiului este S(x)=2x2y = 4x![]() Þ
Þ
Þ S(x) = 4![]() x
x![]() .
.
Derivata
functiei S¢(x) este S¢(x) =![]()
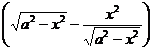 Þ
Þ
Þ S¢(x) =![]()
![]()
Radacinile
derivatei sunt x = ![]() `
`
Cum S(x)
este pozitiva pentru xÎ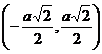 si negativa pentru xÎ
si negativa pentru xÎ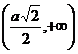 Þ x=
Þ x=![]() este un punct de maxim local.
este un punct de maxim local.
Þ Smax
=2x2y= 4xy Þ Smax=2![]()
![]()
![]() Þ Smax= b
Þ Smax= b![]()
![]() ÞSmax=2ab.
ÞSmax=2ab.
PROBLEMA 3. Sa se determine trunchiul de con circular drept de volum minim, circumscris sferei de raza r.
Solutie.
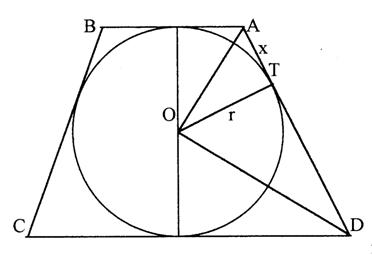
Notand cu x - raza bazei mici a trunchiului
y - raza bazei mari a trunchiului , avem
V=![]() (x2+y2+xy) .
(x2+y2+xy) .
Cum AT=![]() Þ AT=x , DT=
Þ AT=x , DT=![]() Þ DT=y si cum triunghiul AOD avem O=90
Þ DT=y si cum triunghiul AOD avem O=90![]() Þ r2=xy (
conform teoremei inaltimii )
Þ r2=xy (
conform teoremei inaltimii )
Þ
x2y2=r4 Þ y2=![]() Þ
Þ
Þ
V(x)= ![]()
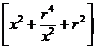 Þ
Þ
Þ
V¢(x)= ![]()
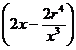 Þ V¢(x)=
Þ V¢(x)= ![]()
![]() Þ
Þ
Þ
V¢(x)=![]()
V¢(x)=0 Þ x=r ; x=-r imposibil (x,r>
|
x |
r +¥ |
|
V¢(x) |
- - - - - - - - - - - - - - - - - - - - - 0 + + + + + + + + + + + + + |
|
V(x) |
|
Þ Vmin se realizeaza cand x=r , adica atunci cand trunchiul de con devine cilindrul circumscris sferei de raza r.
Vmin=![]() (r2+r2+r2) Þ Vmin = 2pr3.
(r2+r2+r2) Þ Vmin = 2pr3.
PROBLEMA 4. In elipsa de ecuatie : 2x2+y2= 18 , se considera punctele A(1,4) si B(3,0). Sa se determine un punct C¹B¢ pe elipsa astfel incat aria triunghilui sa fie maxima.
Solutie. 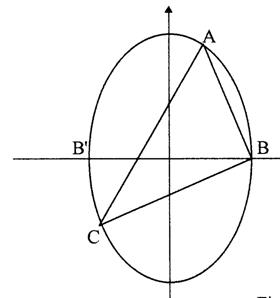
Semiaxele elipsei
sunt : a=3 si b=3![]()
Fie CÎ elipsei Þ C(x, ![]() ).
).
Notand cu
S(x) - aria triunghilui ABC , S :![]() R avem
R avem
S(x)=![]()
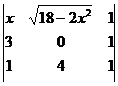 Þ S(x)=6-2x-
Þ S(x)=6-2x-![]() Þ
Þ
Þ
S¢(x)=-2+![]() Þ S¢(x)=
Þ S¢(x)=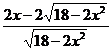

S¢(x)=0 Þ x-![]() =0 Þ x=
=0 Þ x=![]() Þ 3x2=18 Þ x2=6 Þ x=
Þ 3x2=18 Þ x2=6 Þ x=![]()
|
x |
- |
|
S¢(x) |
+ + + + + + + 0 - - - - - - - - - - 0 + + + + + + + + + |
|
S(x) |
|
Smax=S(-![]() )=6+2
)=6+2![]() -
-![]() Þ Smax=6+2
Þ Smax=6+2![]() +
+![]() Þ Smax=6+
Þ Smax=6+![]() .
.
PROBLEMA 5. Sa se determine cilindrul de arie laterala maxima inscris in sfera de raza r.
Solutie. 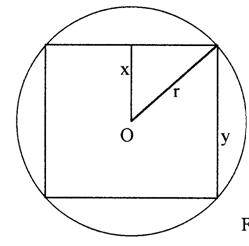
Exprimam generatoarea cilindrului in functie de raza sferei si raza bazei cilindrului , notata cu x si avem ;
g=2![]()
Aria laterala a
cilindrului va fi : S(x)=2px2![]() Þ
Þ
S¢(x)=![]()
S¢(x)=0 Þ x=r![]() g=r
g=r![]() ÞSmax=2pr2.
ÞSmax=2pr2.
PROBLEMA 6. Sa se determine dreptunghiul de arie maxima inscris in cercul de raza r.
Solutie.
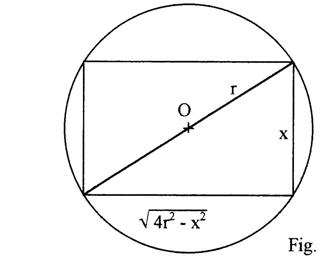
Exprimam aria dreptunghiului in functie de latimea sa x si raza cercului r si avem :
S(x)=x![]()
Þ S¢(x)=![]() . Radacinile
derivatei intai vor fi : S¢(x)=0 Þ x=r
. Radacinile
derivatei intai vor fi : S¢(x)=0 Þ x=r![]()
Deci maximul ariei dreptunghiului inscris se realizeaza pentru patrat si are valoarea : Smax=2r2.
PROBLEMA 7. Sa se determine dreptunghiul de arie maxima inscris in semicercul de raza r, una din laturile sale fiind pe diametrul semicercului.
Solutie.
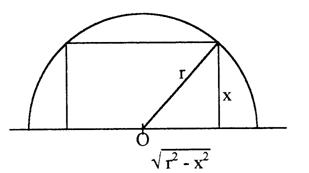
Aria dreptunghilui va
fi : S(x) =2x![]()
Derivata
intai a acestei functii va fi : S¢(x)=![]() . Punand
conditia sa gasim radacinile derivatei, avem :
. Punand
conditia sa gasim radacinile derivatei, avem :
S¢(x)=0 Þ x=r![]() Þ Aria maxima este : Smax=r2.
Þ Aria maxima este : Smax=r2.
Prin urmare, dreptunghiul care rezolva problema are lungimea egala cu dublul latimii.
PROBLEMA 8. Fie ABC un triunghi echilateral cu latura de lungime a. Pe laturile AB, BC, CA luam respectiv punctele C1, A1, B1 astfel incat AC1=BA1=CB1=x . Sa se afle minimul ariei triunghilui echilateral inscris A1B1C1 pentru x variabil.
Solutie.
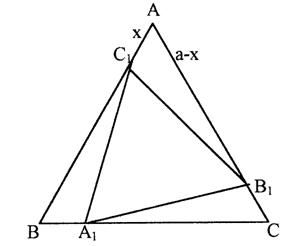
Aria triunghiului AB1C1 se poate exprima cu formula
S(x)=x(a-x)
sin![]() Þ S(x)=x(a-x)
Þ S(x)=x(a-x)![]()
Aria
triunghiului A1B1C1 este : A(x)=a2![]() -x(a-x)
-x(a-x)![]() Þ A(x)=
Þ A(x)=![]() Þ A(x)=
Þ A(x)=![]() (3x2-3ax-a2) Þ
(3x2-3ax-a2) Þ
Þ
A¢(x)= ![]() (6x-3a) Þ A¢(x)=
(6x-3a) Þ A¢(x)=![]() (2x-a).
(2x-a).
Radacina derivatei va fi
x= ![]()
Deci triunghiul de arie minima este triunghiul median al triunghiului echilateral ABC.
PROBLEMA 9. Un cerc are diametrul AB=2a. Pe acest diametru se considera un punct mobil M astfel incat AM=x. Pe segmentele AM si BM luate ca diametrii, se descriu cercurile O1, O2. Sa se afle maximul ariei S(x) a multimii cuprinsa intre cele doua cercuri.
Solutie. 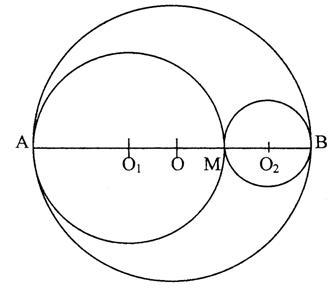
Notam AM=x AB=2a MB=2a-x
S(x)=S1-S2-S3,
unde : S1=pa2 S2=![]() S3=
S3=![]()
Þ S(x)=![]() Þ S(x)=
Þ S(x)=![]()
![]() Þ
Þ
ÞÞS(x)= ![]() (-2x2+4ax) Þ S(x)=
(-2x2+4ax) Þ S(x)=![]() (2a-x), xÎ
(2a-x), xÎ![]()
Avem S(0)=0 si
S(2a)=0 Þ functia S(x) indeplinese conditiile din
teorema lui Rolle Þ cÎ![]() astfel incat S¢(c)=0.
astfel incat S¢(c)=0.
S¢(x)= ![]() (2a-2x) Þ S¢(x)=p(a-x) ÞS¢(x)=0 Þx=a.
(2a-2x) Þ S¢(x)=p(a-x) ÞS¢(x)=0 Þx=a.
Cum S¢(x)=-p <0 funcita
va fi concava pe ![]() Þ S(x) are un maxim dat de
Þ S(x) are un maxim dat de
Smax=S(a)=![]()
PROBLEMA 1. O tinta fixa trebuie atinsa cu un proiectil .Tinta se afla la distanta d pe orizontala si la inaltimea nd ( n>0) fata de punctul de tragere a proiectilului. Neglijand rezistenta aerului, sa se determine viteza initiala minima ce trebuie imprimata proiectilului astfel incat acesta sa atinga tinta.
Solutie. 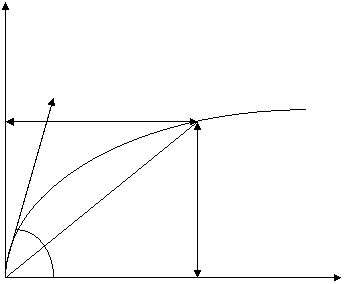
Ecuatia traiectoriei proiectilului in sistemul de referinta xOy este :
y= x tg a -![]() .
.
Dar : x=d ; y=nd., inlocuind in ecuatia traiectoriei si explicitand pe v0 se obtine :
v02
= ![]() aÎ
aÎ![]()
Pentru determinarea extremelor functiei v0 =f(a), avem :
f¢ a ![]()
Exprimand in relatia de mai sus toate functiile trigonometrice prin tg a se obtine :
f¢ a ![]()
Cautam punctele de extrem si pentru aceasta egalam derivata cu 0 obtinand ecuatiile :
tg2a sau tg2a-2n tga
Prima ecuatie nu are solutii reale, deci acceptabile.Pentru a doua ecuatie avem solutiile :
tg a =n ![]()
Deoarece aÎ![]() numai solutia tga =n+
numai solutia tga =n+![]() satisface problema.Facand tabelul de variatie al
derivatei ,obtinem punctele de extrem ale functiei
satisface problema.Facand tabelul de variatie al
derivatei ,obtinem punctele de extrem ale functiei
|
a |
tga tga |
|
f¢ a |
+ + + + 0 - - - - - - 0 + + + + + |
|
f(a |
|
Din tabelul de semn al derivatei se deduce ca tga este punct de
minim al functiei v0=f(a) iar valoarea
functiei in punctul de minim se obtine inlocuind tga =n+![]() in functie :
in functie :
v![]()
![]()
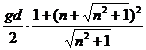 =gd(n+
=gd(n+![]()
v![]()
![]()
PROBLEMA 2. Se da un canal hidraulic cu sectiunea trapezoidala de arie constanta . Cunoscand ca panta taluzului este constanta , tg a=m=1, sa se determine raportul dintre baza mica si inaltimea sectiunii trapezoidale a canalului hidraulic , astfel incat sa rezulte perimetrul minim dat.
Solutie.
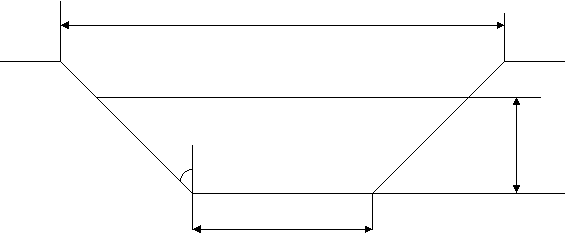
Notand cu h si respectiv cu b, inaltimea si respectiv baza mica a sectiunii trapezoidale a canalului hidraulic , perimetrul udat este :
P=b+![]()
Cum insa
cos a 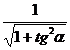 (0<a<
(0<a<![]() ) si cum tg a=m, avem
) si cum tg a=m, avem
P=b+2h![]()
Notand ![]() = x, rezulta :
= x, rezulta :
P=h(x+2![]()
Pe de alta parte aria sectiunii canaluluii este :
A=h(b+mh),
Sau
A=h2(x+m)
Din care :
h=![]() , (h>
, (h>
Inlocuind inexpresia perimetrului, avem :
P=![]() (x+2
(x+2![]()
Deoarece A si m sunt constante , rezulta ca P prezinta un extrem cand P¢(x)=0.
P¢(x)=![]()
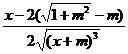
Rezulta
x=2(![]() -m) sau x
-m) sau x![]()
Pentru a stabili natura punctului de extrem calculam valoarea derivatei secunde si comparam cu zero.
P²(x)=![]()
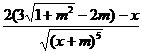
Inlocuind valoarea punctului de extrem in derivata secunda,avem ;
P²(x0=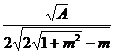 >
>
Deci pentru x dat de
relatia x=2(![]() -m), P prezinta un minim.
-m), P prezinta un minim.
Valoarea minima a perimetrului udat, este :
Pmin=2![]()
Sau Pmin![]()
![]()
PROBLEMA 3. Doi purtatori de sarcina electrica pozitiva de aceeasi valoare Q, punctiformi , sunt asezati in varfurile B si C ale unui triunghi isoscel ABC (B=C) .Se cere sa se determine valoarea unghiului A pentru care intensitatea campului electrostatic de cei doi purtatori de sarcina in varful A are valoarea maxima. Latura BC a triunghiului are marimea d.
Solutie.
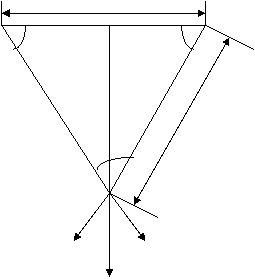
Notam B=C=a iar A=b
Intensitatea campului electric creat de cele doua sarcini in varful A al triunghiului este :
E=E1cos ![]() , in care E1=
, in care E1=![]() , r=
, r=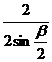
Inlocuind in expresia intensitatii capului electric , se obtine :
E=![]() sin2
sin2![]() cos
cos ![]()
Este necesar a se gasi extremele functiei E=f(b).Avem :
E¢ b ![]() sin
sin![]() (2 cos2
(2 cos2![]() -sin2
-sin2![]()
Solutiile ecuatiei E¢ b)=0 sunt :
sin ![]() =0 Þ b
=0 Þ b
si tg2![]() =2 Þ tg
=2 Þ tg ![]()
![]()
din care tg ![]()
![]() Þ b
Þ b ![]() ¢
¢
tg ![]()
![]() Þ b
Þ b ![]() ¢
¢
Este usor de observat ca
numai soluitia b ![]() ¢ ;este
acceptabila , deoarece b =0 conduce la E
=0, fapt ce semnifica ca punctul A se gaseste la infinit pe perpendiculara ce
cade pe mijlocul lui BC , iar b
¢ ;este
acceptabila , deoarece b =0 conduce la E
=0, fapt ce semnifica ca punctul A se gaseste la infinit pe perpendiculara ce
cade pe mijlocul lui BC , iar b ![]() ¢ este
inacceptabila din punct de vedere geometric. Pentru solutia b =0 se obtine de
fapt valoarea minima a lui E.
¢ este
inacceptabila din punct de vedere geometric. Pentru solutia b =0 se obtine de
fapt valoarea minima a lui E.
Pentru a determina natura extremu lui dat de b , avem :
E² b ![]() cos
cos ![]()
![]()
Tinand
seama ca sin![]()
![]() si cos
si cos ![]()
![]() , rezulta ca E² b) pentru b b
este :
, rezulta ca E² b) pentru b b
este :
E² b ![]() <
<
Deci pentru b b , E =f(b) prezinta un maxim a carui valoare rezulta inlocuind b
Emax=![]()
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |