
OSCILATORUL ARMONIC CA AMPLIFICATOR CU REACTIE POZITIVA
In studiul oscilatoarelor armonice exista diferite metode de abordare care sa ne permita determinarea conditiilor de oscilatie, a tensiunii de iesire si a variantelor posibile de implementare. O prima metoda de abordare a unui oscilator este cea de amplificator cu reactie pozitiva. Schema bloc, sistemul de ecuatii si graful Mason asociat acestuia in cazul unei astfel de abordari sunt prezente in fig. 2.
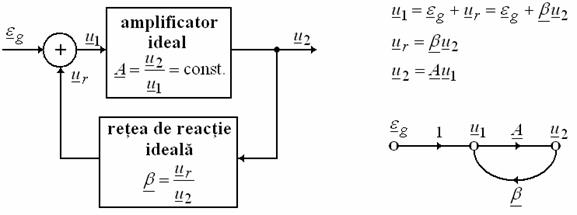
Fig. 2 Oscilatorul armonic ca amplificator cu reactie pozitiva
Reamintim ca, in cazul grafului Mason, determinantul sistemului se determina ca:
![]() (3)
(3)
unde: ![]() reprezinta suma
transmitantelor buclelor simple;
reprezinta suma
transmitantelor buclelor simple; ![]() reprezinta suma
tuturor produselor intre transmitantele perechilor de bucle neadiacente;
reprezinta suma
tuturor produselor intre transmitantele perechilor de bucle neadiacente; ![]() reprezinta suma
tuturor produselor intre transmitantele a trei cupluri de bucle
neadiacente s.a.m.d., iar transferul de la un nod sursa la un nod
sarcina se determina ca:
reprezinta suma
tuturor produselor intre transmitantele a trei cupluri de bucle
neadiacente s.a.m.d., iar transferul de la un nod sursa la un nod
sarcina se determina ca:
![]() , (4)
, (4)
unde ![]() reprezinta o cale
de la nodul sursa la un nodul sarcina, iar
reprezinta o cale
de la nodul sursa la un nodul sarcina, iar ![]() - minorul caii
respective, care se determina ca si Δ, luand insa in
considerare numai buclele neadiacente caii respective.
- minorul caii
respective, care se determina ca si Δ, luand insa in
considerare numai buclele neadiacente caii respective.
In aceste conditii vom obtine:
determinantul grafului: ![]()
amplificarea cu reactie: 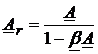 .
.
Conform conditiei necesare si suficiente (2), circuitul oscileaza daca Δ=0. Rezulta conditia de oscilatie, cunoscuta si ca relatia Barkhausen:
![]() . (5)
. (5)
Deoarece in circuit exista elemente reactive, putem scrie:
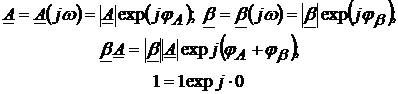
Din analiza relatiilor de mai sus rezulta ca relatia lui Barkhausen este echivalenta cu doua conditii reale:
conditia de
amplitudine ![]() ; (6)
; (6)
conditia de faza ![]() sau
sau ![]() (7)
(7)
In multe situatii
practice A este real, iar ![]() in cazul unui amplificator
neinversor sau
in cazul unui amplificator
neinversor sau ![]() in cazul unui amplificator
inversor. In astfel de situatii rezulta ca reteaua de
reactie este cea care satbileste frecventa de oscilatie,
aceasta putand fi determinata din relatia:
in cazul unui amplificator
inversor. In astfel de situatii rezulta ca reteaua de
reactie este cea care satbileste frecventa de oscilatie,
aceasta putand fi determinata din relatia:
![]() . (8)
. (8)
Pentru caracterizarea unui oscilator trebuie sa cunoastem:
a) conditia de amorsare a oscilatiilor;
b) frecventa de oscilatie ![]() ;
;
c) amplitudinea oscilatiilor: Uosc;
d) conditia de stabilitate dinamica a oscilatiilor.
Conditia de amorsare a oscilatiilor si frecventa de oscilatie pot fi determinate folosind teoria liniara a oscilatoarelor, bazata pe modelul de semnal mic al elementului activ. In conditiile mentionate mai sus, frecventa de oscilatie se va determina din relatia (8), iar pentru sustinerea oscilatiilor va fi necesar ca:
![]() . (
. (
Pentru determinarea amplitudinii
oscilatiilor se poate face apel la teoria cvasiliniara, liniarizand
EA pe portiuni si la metoda frecventei fundamentale folosite la
studiul amplificatoarelor de radiofrecventa de putere. Cunoscand
tensiunea maxima de iesire si de excitatie, specifice
clasei de functionare a elementului activ utilizat (A, A-B sau C), putem
stabili valoarea amplificarii in tensiune la frecventa de
rezonanta, ![]() , iar din (9) deducem valoarea lui
, iar din (9) deducem valoarea lui ![]() necesara
sustinerii oscilatiilor.
necesara
sustinerii oscilatiilor.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |