Theoretical, experimental and numerical investigations of the flow generated by a 3D spinning disk

ABSTRACT

The work is concerned with the numerical and experimental investigations of the flow generated by a disk in rotational motion. The main goal of the present study is to validate the 3D numerical solutions obtained with FLUENT code. Numerical computed streamlines and pressure distributions, respectively the dependence of the torque coefficient on the Reynolds number, are compared with experimental data and analytical solutions. We also analyze different techniques to put in evidence the vortical structures and the areas within the flow domain where the intensity of the vortices reach high values. In this respect, we introduce a novel "user defined function", respectively the vorticity number (W₀), as a key component to emphasis the local vortex intensity. One can conclude that the obtained 3D numerical solution offers a very good representation of the real phenomena and provides additional value information about the structure of the flow field. The further step is focused to the implementation within the numerical code of a novel rheological model with variable time viscosity. The final target of the study is to simulate the dynamics of a chemical reactor during the polymerization reaction.

Keywords: CFD, hydrodynamics, spinning disk, vorticity number

NOMENCLATURE

characteristic length [m]

pressure [Pa]

velocity [m/s]

gas density [kg/m³]

dynamic viscosity [kg/m.s]

INTRODUCTION

Mixing is a dynamic process whose driving force is the pressure difference in various tank regions that is produced by a rotating impeller [1]. The same principle applies to a rotating disk, with the obvious difference that the transformation of mechanical energy supplied by the impeller into kinetic energy of liquid in the tank is much more efficient. Therefore, the use of a rotating disk for the mixing process cannot induce a turbulent motion, which limits the research to a range of Reynolds numbers - Re I

The study has been performed prior to the hydrodynamics study of a chemical reactor for two reasons: (i) numerical code validation; (ii) experimental and numerical description of the phenomena induced by the spinning disk. It is fundamental to understand the basics of a phenomenon to be able to take the research further and further. The validation of the FLUENT code has been performed considering the experimental results, the 3D numerical solutions and also analytical solutions from the literature.

In the interest of good results, the geometry used for the experiments has been recreated numerically. The experiments were performed on a PHISICA RHEOLAB MC1 rheometer using a spinning disk in an enclosed chamber with the dimensions presented in Figure 1.

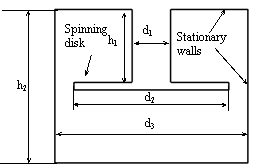
Figure 1: Schematic diagram of the mixing geometry with:

h₁ = 19 mm; h₂ = 40 mm; d₁ = 10 mm; d₂ = 40 mm; d₃ = 50 mm.

Model description

The numerical approach of the study is based on the configuration of the experimental set-up. All the numerical simulations have been performed in the FLUENT code, with the primary objective of validating the code. Generating a 3D geometry implies the use of one or a combination of several techniques in Computer Aided Design (CAD). Due to the fact that GAMBIT is the recommended pre-processor for FLUENT, and that the geometry is not very complicated, we were able to create it, using the volume generating commands and a series of Boolean operations from GAMBIT(Figure 2).

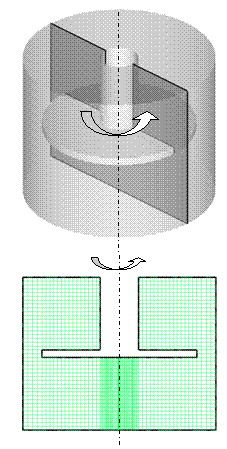
Figure 2: 3D model of the mixing chamber with 2D slice of the mesh

The current simulation introduces a small problem in the mesh generation. The asymmetry of the upper and lower geometry in relation with the disk implies that the automated mesh generation schemes implemented in the pre-processor will not work properly. So, in order to obtain a reliable mesh, the use of additional helping constructing elements was necessary. To have a good convergence and a high precision of the numerical solutions, a structured mesh has been generated (Figure 2), using a Cooper scheme [2]. The 3D mesh contains 119226 hexahedral cells (Figure 3).

Figure 3: 3D mesh generated with the Cooper scheme

The numerical studies have been performed in a range of Reynolds numbers - Re I (Navier-Stokes solutions of Newtonian fluid using the laminar solver).

Reynolds number

RESULTS

The experiments have been performed in the REOROM Laboratory from P.U. Bucharest. The mixing chamber with the components: the enclosed cylinder and the shaft link to the disk, was installed on a PHISICA RHEOLAB MC1 rheometer. In addition, to obtain a visualisation of the flow in the vicinity of the disk, a laser beam was focused on the median plane of the cylinder. Due to the rotational speed limits of the rheometer (n I rot/min) and the fixed dimensions of the geometry, we used a low viscosity fluid, in order to obtain the designated range for Reynolds number. The fluid used was water with the following material properties: η = 1 mPa.s, ρ = 1000 kg/m³. For the visualizations, in the fluid were introduced small particles of allumina powder (20÷40 microns) to deflect the light and show the streamlines. The digital camera used for the experiments was a Minolta Dimage 7 with macro lens, set to 2s exposure time to properly obtain the streamlines + the laser.

The representative visualization of the streamlines generated by the 3D spinning disk is at Re = 1000 (Figure 4). The good correlation between the experimental visualization and the predicted streamline distribution is evident. The lower vortex is very well defined in both representations and is one of the first steps and criteria for the numerical code validation.

Figure 4: Experimental streamlines visualization compared with numerical streamlines distribution at Re=1000

Alongside the streamlines distribution, the pressure distribution comes to sustain the visual analysis of the flow patterns (Figure 5). The pressure gradients describe quite well the dynamic process of mixing.

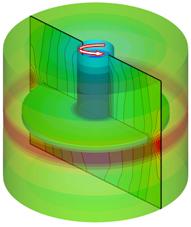
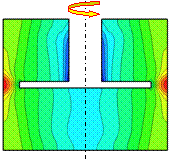
Figure 5: 3D and 2D median plane distribution of pressure at Re=1000

A second criteria used for the numerical code validation is a diagram of the moment coefficient in relation with the Reynolds number (Figure 6). The diagram contains results from three sources: experiments, numerics and literature. Because the torque transducer installed on the rheometer is not sensitive enough, the range of Reynolds numbers for the experimental data is 100÷1000. The formulation for the moment coefficient is given by the (2) formula. In the literature, there are two other formulation of the moment coefficient: Cochran's (3) and Müller's (4)[ ]. Both are based on the Reynolds number and deal with the flow within the laminar flow regime. But each one of them is more efficient on certain areas of the flow domain. Cochran's formulation characterizes the flow very well for Re = 1÷10, with an extension towards Re = 30. On the other hand, Müller's formulation describes perfectly the flow for Re = 100÷1000, with extensions towards Re = 50.

Moment coefficient

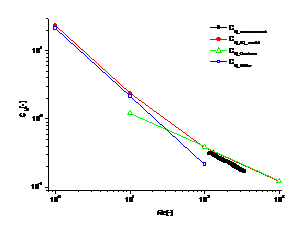
Figure 6: Moment coefficient diagram for theoretical, experimental and numerical results

Figura ceva mai mare (la scris!!!!).

We also analyze different techniques to put in evidence the vortical structures and the areas within the flow domain where the intensity of the vortices reach high values. In this respect, we introduce a novel "user defined function", respectively the vorticity number (Wo), as a key component to emphasis the local vortex intensity.

Vorticity number is the balance between rotation and deformation of a fluid particle, defined as the ratio between the magnitude of Ω and the magnitude of D (5).

In the flow areas were Wo > 1 vortices are present, this constrain being considered one first criteria for vortex existence [3].

The distribution of Wo from Figure 7 evidences the regions where possible vortices might be present; respectively the domains with Wo > 1, coincide with the vortices location.

Figure 7: Vorticity number distribution for Wo > 1

Based on this novel "user defined function", which we implemented in the FLUENT code, we define a new way of quantification for the mixing process: a mixing coefficient (C_x). The mixing coefficient C_x is defined by the ratio between the volume of the fluid characterized by Wo > 1 and the total volume of the fluid (6). In the table 1 are presented the values of the volume ratio in the range Re = 1÷1000, for steady state flow - C_x-a and for unsteady flows - C_x-b, with the variation of Reynolds number in time.

CONCLUSION

According to the visual analysis, alongside the diagram of the moment coefficient in relation with the Reynolds number, the numerical code validation was a success. The theoretical, experimental and numerical results were in very good correlation, establishing the bases for future, more complicated research cases. More than that, due to the fact that numerical simulations can provide additional data, we are able to find new ways of characterizing the phenomena.

Further research is focused to the implementation of a novel rheological model with variable time viscosity. The final target of the study is to simulate the dynamics of a chemical reactor during the polymerization reaction.

ACKNOWLEDGMENTS

The present work has been performed under the guidance of dr. ing. Sebastian MUNTEAN, at the National Center for Engineering of Systems with Complex Fluids, "Politehnica" University of Timisoara.

CNCSIS-ul tau de asemenea

REFERENCES

C. KUNCEWICZ, K. SZULC, T. KURASINSKI Hydrodynamics of the tank with a screw impeller Chemical Engineering and Processing 44,

C. MARCULESCU, C. BALAN, "Numerical solutions of a 3d spinning disk, using different geometry and mesh generation techniques", Computer aided engineering solutions for design, analysis and innovation (ANSYS & FLUENT user group meeting), April 2007, Sinaia, Romania

D. BROBOANA, A. CALIN, C. MARCULESCU, C. BALAN, "Vortical structures at the interface", 2^nd Workshop on Vortex Dominated Flows - Achievements and Open Problems, Bucharest, Romania, 2006