Functia de gradul al II-lea
![]() Avand
date numerele reale a,b,c cu a nenul ,
functia f:R→R definita prin f(x)=ax2+bx+c se
numeste functie de gradul al II-lea cu coeficienti a,b,c.
Avand
date numerele reale a,b,c cu a nenul ,
functia f:R→R definita prin f(x)=ax2+bx+c se
numeste functie de gradul al II-lea cu coeficienti a,b,c.
![]() Forma
canonica a functiei :f(x)=a
Forma
canonica a functiei :f(x)=a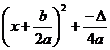
![]() Puncte
de extrem ale functiei de gradul al II-lea :
Puncte
de extrem ale functiei de gradul al II-lea :
1)Daca a>0 atunci f
are un punct de minim m![]()
2) Daca a<0 atunci f
are un punct de maxim M![]()
![]() Monotonia
functiei de gradul al II-lea
Monotonia
functiei de gradul al II-lea
1) Daca a >0 atunci
|
x |
|
|
f(x) |
|
2) Daca a<0 atunci
|
x |
|
|
f(x) |
|
![]() Graficul
functiei de gradul al II-lea -este o parabola
Graficul
functiei de gradul al II-lea -este o parabola
Etapele construirii graficului functiei de gradul al II-lea:
1) Intersectia cu axa Ox : este data de semnul lui ∆
Daca ∆>0 atunci graficul intersecteaza axa Ox in 2 puncte A(x1;0) si B(x2;0) unde x1si x2 sunt radacinile ecuatiei ax2+bx+c=0
Daca ∆=0 atunci
graficul intersecteaza axa Ox intr-un singur punct V(![]() ) .Graficul este tangent axei Ox .
) .Graficul este tangent axei Ox .
Daca ∆<0 atunci graficul nu intersecteaza axa Ox.
Intersectia cu axa Oy : graficul functiei intersecteaza axa Oy in punctul C(0;c)
2) Varful parabobolei V![]()
3)Axa de simetrie dreapta x=![]()
4) Tabelul de variatie ( din care rezulta punctele prin care trece graficul si monotonia functiei)
5) Trasarea graficului.
![]() Semnul
functiei de gradul al II-lea
Semnul
functiei de gradul al II-lea
1) Daca ∆<0 functia pastreaza semn constant - semnul lui a
|
x |
∞ |
|
f(x) |
semnul lui a |
2) Daca ∆=0 functia pastreaza semn constant - semnul lui a si se anuleaza intr-un punct
|
x |
|
|
f(x) |
semnul lui a 0 semnul lui a |
3) Daca ∆>0 atunci functia prezinta alternanta de semn
|
x |
x1 x2 ∞ |
|
f(x) |
semnul lui a 0 semn contrar lui a 0 semnul lui a |
![]() Inecuatiile
de gradul al II-lea se rezolva cu ajutorul semnului functiei de
gradul al II-lea intocmind un tabel de semn.
Inecuatiile
de gradul al II-lea se rezolva cu ajutorul semnului functiei de
gradul al II-lea intocmind un tabel de semn.
![]() Pozitia
radacinilor ecuatiei de gradul al II-lea in raport cu un
numar real α
Pozitia
radacinilor ecuatiei de gradul al II-lea in raport cu un
numar real α
Fie f(x)=ax2+bx+c avand radacinile x1si x2
1) x1<x2<α daca sunt indeplinite conditiile :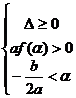
2) α<x1<x2
daca sunt indeplinite conditiile :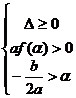
3)x1<α<x2
daca sunt indeplinite conditiile :![]()
Pozitia radacinilor ecuatiei de gradul al II-lea fata de un numar real α se putea aborda si notand cu y1=x1-α cu y2=x2-α ( adica se face transformarea y=x-α → x=y+α) caz in care semnul radacinilor ecuatiei in y da pozitia radacinilor ecuatiei in x fata de numarul α.
![]() Alte
aplicatii ale functiei de gradul al II-lea :-conditii ca o
expresie de gradul al II-lea sa aiba acelasi semn pe un interval
Alte
aplicatii ale functiei de gradul al II-lea :-conditii ca o
expresie de gradul al II-lea sa aiba acelasi semn pe un interval
-familii de parabole :-determinarea curbei descrisa de varfurile unei familii de parabole
-determinarea punctului fix al unei familii de parabole
-determinarea imaginii sau multimii valorilor unei functii
![]() Sisteme
de ecuatii neliniare
Sisteme
de ecuatii neliniare
1) Sisteme formate dintr-o ecuatie de gradul I si o ecuatie de gradul al II-lea :
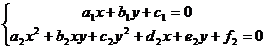
Procedeu : se substituie x sau y din prima ecuatie si se introduce in a doua ecuatie obtinandu-se o ecuatie de gradul al II-lea numai in x sau numai in y
2) Sisteme omogene
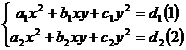
Procedeu : Daca d1≠0
si d2≠0 , se inmulteste ecuatia (1) cu d2
si ecuatia (2) cu (-d1), se aduna si se
obtine o ecuatie omogena
de gradul al II-lea cu termenul liber 0.Impartind ecuatia
omogena la y2 (y=0 nu este solutie a sistemului ),
obtinem o ecuatie de gradul al II-lea cu necunoscuta t =![]() . Sistemul se reduce
astfel la doua sisteme de tipul 1.Daca d1≠0 si
d2=0 ,se imparte ecuatia (2) prin y2 si se
formeaza ecuatia de gradul al II-lea cu necunoscuta t=
. Sistemul se reduce
astfel la doua sisteme de tipul 1.Daca d1≠0 si
d2=0 ,se imparte ecuatia (2) prin y2 si se
formeaza ecuatia de gradul al II-lea cu necunoscuta t=![]()
3) Sisteme simetrice (sistemele care nu se schimba daca inlocuim pe x cu y si pe y cu x)
Procedeu : se introduc necunoscutele auxiliare s si p date de relatiile x+y=s si xy=p. Sunt utile identitatile :
x2+y2=(x+y)2-2xy=s2-2p
x3+y3= (x+y)3-3xy(x+y)=s3-3sp
x4+y4=(x2+y2)-2x2y2=(s2-2p)2-2p2
![]() In
rezolvarea ecuatiilor sau inecuatiilor daca apar module se
expliciteaza modulele si se analizeaza cazurile care apar.De
multe ori este util sa se tina cont de proprietatile
modulului.
In
rezolvarea ecuatiilor sau inecuatiilor daca apar module se
expliciteaza modulele si se analizeaza cazurile care apar.De
multe ori este util sa se tina cont de proprietatile
modulului.
![]() Ecuatiile
in care necunoscuta apare sub radicali
se numesc ecuatii irationale.In rezolvarea lor este bine sa se
parcurga etapele:1)conditii de existenta si de
compatibilitate(conditiile de compatibilitate se pot adauga si
pe parcursul rezolvarii ecuatiei)
Ecuatiile
in care necunoscuta apare sub radicali
se numesc ecuatii irationale.In rezolvarea lor este bine sa se
parcurga etapele:1)conditii de existenta si de
compatibilitate(conditiile de compatibilitate se pot adauga si
pe parcursul rezolvarii ecuatiei)
2)eliminarea radicalilor prin -ridicare la putere
-amplificare cu expresia conjugata
-utilizarea diferitelor substitutii
3)rezolvarea ecuatiei obtinute
4)verificarea solutiilor obtinute in ecuatia initiala.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |