
Transformari rectangulare - transformata Hadamard - Probleme rezolvate
Fie urmatorul bloc U de 4×4 pixeli dintr-o imagine digitala, in care fiecare pixel este reprezentat prin luminanta sa - o valoare intreaga in multimea :
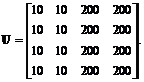
a) Calculati transformata Hadamard 2-D a blocului, folosind matricea transformatei Hadamard ordonata, de dimensiune 4×4, H4,ord[4×4].
b) Demonstrati conservarea energiei in domeniul transformat.
c) Examinati compactarea energiei blocului in domeniul transformat, in comparatie cu distributia energiei blocului in domeniul original.
Rezolvare:
a) Matricea transformarii Hadamard de dimensiune N×N, pentru N - o putere a lui 2 oarecare, N=2n, cu n - intreg pozitiv supraunitar, se obtine recursiv din matricea de ordin imediat inferior N-1, conform ecuatiei:
![]() pentru
N>2
pentru
N>2
(respectiv, este ![]() pentru N=2).
pentru N=2).
Aceasta este expresia matricei transformarii Hadamard in forma sa neordonata. In forma ordonata, se obtine matricea transformarii HN,ord prin rearanjarea liniilor matricii HN in ordine crescatoare a nr. de schimbari de semn pe linie (secventei liniilor).
Atunci, pentru N=4, obtinem:
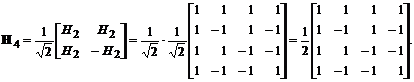
Cum numarul de schimbari de semn in H4 este 0 in prima linie, 3 in a 2-a linie, 1 in a 3-a linie si 2in ultima linie, H4,ord se obtine prin mutarea liniei 3 pe a 2-a pozitie, mutarea liniei 4 pe a 3-a pozitie si mutarea liniei 2 pe ultima pozitie:
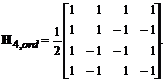
Transformata Hadamard 2-D ordonata a blocului se obtine din inmultirea matriciala (care defineste forma generala a transformarii directe a unui bloc de imagine, exprimata sub forma matriciala):
![]() .
.
Matricea
transformarii Hadamard (in oricare din forme, ordonata sau neordonata)
este simetrica, ![]() (se poate observa ca
prima linie si prima coloana sunt identice, a doua linie si a doua coloana sunt
identice, a treia linie si a treia coloana sunt identice, si la fel, a patra
linie si a patra coloana). Ca urmare, transformarea directa se poate rescrie
sub forma:
(se poate observa ca
prima linie si prima coloana sunt identice, a doua linie si a doua coloana sunt
identice, a treia linie si a treia coloana sunt identice, si la fel, a patra
linie si a patra coloana). Ca urmare, transformarea directa se poate rescrie
sub forma:
![]()
Putem calcula
intai oricare din produsele matriciale din ecuatia de mai sus, urmand sa
inmultim rezultatul inca o data (fie la stanga, fie la dreapta, in functie de
ordinea aleasa) cu matricea H4,ord. De
exemplu, daca alegem sa calculam intai ![]() , obtinem:
, obtinem:
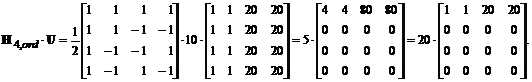
Apoi, inmultind acest rezultat la dreapta cu H4,ord, obtinem blocul transformat V cu coeficientii:
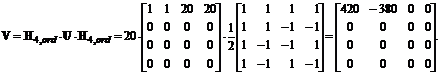
b) Demonstrarea conservarii energiei in domeniul transformat inseamna verificarea faptului ca energia blocului U se regaseste in totalitate in varianta sa transformata V. In general, energia unui bloc de imagine se calculeaza ca suma patratelor valorilor luminantelor din bloc, iar energia blocului transformat - ca suma patratelor modulelor coeficientilor (identice cu patratele coeficientilor pentru transformari reale). Ca urmare, putem calcula energia EU in blocul de imagine original si energia EV in blocul de imagine reprezentat in domeniul transformat cu ecuatiile:
![]()
unde u(m,n) = luminanta pixelului de pe linia m si coloana n din blocul U, respectiv:
![]()
unde v(k,l) = valoarea coeficientului de pe linia k si coloana l din blocul transformat V.
Verificarea conservarii energiei inseamna verificarea respectarii
relatiei ![]() (ecuatia conservarii
energiei blocului in urma transformarii).
(ecuatia conservarii
energiei blocului in urma transformarii).
Numeric, calculam:
![]()
![]()
Ca urmare ![]() , deci se conserva energia blocului in urma transformarii
(transformarea este cu conservare a energiei, ceea ce ne indica faptul ca putem
reconstitui oricand - prin transformare inversa - fara distorsiuni, blocul
original de pixeli din reprezentarea sa in domeniul transformat).
, deci se conserva energia blocului in urma transformarii
(transformarea este cu conservare a energiei, ceea ce ne indica faptul ca putem
reconstitui oricand - prin transformare inversa - fara distorsiuni, blocul
original de pixeli din reprezentarea sa in domeniul transformat).
Observatie: O modalitate alternativa de demonstrare a conservarii energiei este cea bazata pe proprietatea transformarilor unitare de a conserva energia blocurilor pe care le transforma. Ca urmare, daca putem demonstra ca matricea transformarii H4,ord este unitara, folosind proprietatea mentionata, va fi demonstrata automat si conservarea energiei.
O matrice este unitara daca inversa sa este egala cu complex conjugata transpusei sale. Una dintre proprietatile transformarii Hadamard este faptul ca matricea transformarii este unitara, ca urmare acest lucru garanteaza conservarea energiei imaginii in domeniul transformat.
c) Compactarea energiei blocului in domeniul transformat, in comparatie cu distributia energiei blocului in domeniul original, este data de numarul de coeficienti nuli sau foarte mici in comparatie cu coeficientii din blocul original. In blocul original, nu avem nici un coeficient nul, ca urmare putem estima energia necompactata deloc (ci distribuita intre cei 16 coeficienti). Daca examinam in schimb blocul V, observam ca doar doi coeficienti sunt nenuli (si mai mari desigur decat coeficientii/luminantele din blocul original U). Ca urmare, energia este compactata in domeniul transformat in 2 din totalul de 16 coeficienti ai blocului. Avem deci prin transformare o compactare a energiei in 2/16 din coeficienti, adica in 12.5% din coeficienti - deci putem spune ca transformarea a fost eficienta din perspectiva compactarii energiei.
Care dintre urmatoarele matrici pot fi folosite pentru transformarea bidimensionala unitara separabila rectangulara a unui bloc de imagine U de dimensiune 4×4 pixeli, cu pixelii reprezentati prin luminantele lor? Justificati raspunsul.
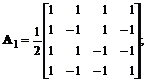
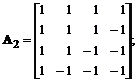
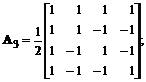
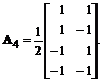
Rezolvare:
Sub forma matriciala, orice transformare bidimensionala separabila a unui bloc de imagine descris de o matrice patratica (cu pixelii sai reprezentati prin valori scalare - luminante), bloc U[N×N], se descrie prin ecuatia:
![]()
unde A este matricea transformarii, care trebuie sa aiba aceeasi dimensiune ca si blocul U, in cazul unui bloc patratic (cu numar egal de linii si coloane), adica A[N×N]. In cazul nostru, dimensiunea blocului U fiind 4×4 pixeli, N=4, deci matricea A trebuie sa fie de dimensiune 4×4 pentru a putea implementa transformarea bidimensionala separabila descrisa de ecuatia matriciala anterioara. Matricile A1, A2 si A3 satisfac aceasta conditie; singura matrice care nu satisface conditia este A4.
Daca transformarea trebuie sa fie si unitara, atunci matricea A trebuie sa fie unitara, adica inversa ei trebuie sa fie complex conjugata transpusa,
![]()
Ca urmare, pentru matricile ramase posibile candidate pentru implementarea transformarii bidimensionale unitare separabile, trebuie sa verificam daca ele satisfac conditia de a fi unitare sau nu (respectiv, care dintre ele este unitara).
Toate
cele trei matrici de dimensiune 4×4 sunt reale, ca urmare, complex conjugarea
nu are efect, adica, ![]()
![]()
![]() Vom calcula pentru
fiecare din cele trei matrici produsul
Vom calcula pentru
fiecare din cele trei matrici produsul ![]()
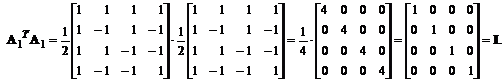
Ca urmare, matricea A1 este unitara, deci poate fi folosita pentru implementarea unei transformari unitare bidimensionale.
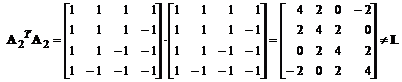
Ca urmare, matricea A2 nu este unitara, deci nu poate fi folosita pentru implementarea unei transformari unitare bidimensionale.

Ca urmare, si matricea A3 este unitara, deci si ea poate fi folosita pentru implementarea unei transformari unitare bidimensionale.
Ambele matrici A1 si A3 au pe liniile lor functii rectangulare discrete (liniile acestor matrici sunt de tip semnal dreptunghiular), ca urmare oricare din ele indeplinesc toate conditiile necesare pentru a implementa o transformare bidimensionala unitara separabila rectangulara a unui bloc de imagine U de dimensiune 4×4 pixeli.
Fie blocul U de 4 4 pixeli dintr-o imagine digitala, in care fiecare pixel este reprezentat prin luminanta sa in domeniul , si fie matricea transformarii Hadamard H [4 4], definite prin:
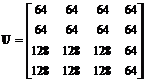 ;
; 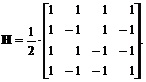
a) Cum arata matricea transformarii Hadamard ordonate dupa numarul de schimbari de semn? Demonstrati ca aceasta matrice este unitara.
b) Calculati transformata Hadamard bidimensionala a blocului U, folosind fie matricea transformarii Hadamard ordonate, fie cea data in enunt.
c) Demonstrati conservarea energiei imaginii prin aceasta transformare si examinati compactarea energiei imaginii in domeniul transformat fata de cel original, prin estimarea numarului de coeficienti nenuli din imaginea reprezentata in domeniul transformat comparativ la numarul total de pixeli din imagine.
Rezolvare:
a) Matricea transformarii Hadamard date in enunt prezinta:
zero schimbari de semn pe prima linie;
trei schimbari de semn pe a doua linie;
o schimbare de semn pe a treia linie;
doua schimbari de semn pe ultima linie,
deci nu are liniile ordonate crescator ca si numar de schimbari de semn pe linie (secventa a liniei, sau, frecventa a semnalelor (vectorilor) de baza).
Pentru obtinerea matricii transformarii Hadamard ordonate dupa numarul de schimbari de semn pe linii, trebuie reordonate liniile prin:
mutarea liniei doi din H de mai sus pe pozitia patru (devine ultima linie in matricea ordonata);
mutarea liniei trei din H de mai sus pe pozitia doi (devine a doua linie in matricea ordonata);
mutarea liniei patru din H pe pozitia trei (devine a treia linie in matricea ordonata).
Obtinem astfel matricea ordonata dupa numarul de schimbari de semn pe linii notata prin Hord[4×4]:
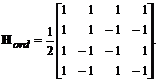
Demonstrarea faptului ca Hord este unitara se reduce la a demonstra ca:
![]()
Matricea Hord
este reala, ca urmare 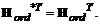 In plus, Hord
este si simetrica (prima linie egala cu prima coloana; a
doua linie egala cu a doua coloana; a treia linie egala cu a
treia coloana; a patra linie egala cu a patra coloana), deci
In plus, Hord
este si simetrica (prima linie egala cu prima coloana; a
doua linie egala cu a doua coloana; a treia linie egala cu a
treia coloana; a patra linie egala cu a patra coloana), deci ![]() Atunci, trebuie
sa demonstram ca
Atunci, trebuie
sa demonstram ca ![]() pentru ca Hord
sa fie unitara. Calculam acest produs matricial:
pentru ca Hord
sa fie unitara. Calculam acest produs matricial:
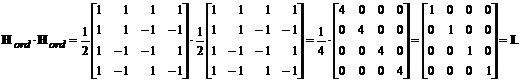
Produsul fiind matricea identitate de dimensiune 4×4, inseamna ca matricea transformarii Hord data mai sus este unitara.
b) Transformata Hadamard 2-D a blocului se obtine din inmultirea matriciala (care defineste forma generala a transformarii directe a unui bloc de imagine, exprimata sub forma matriciala) fie cu Hord, fie cu H. Alegem aici sa lucram cu Hord:
![]() .
.
Putem calcula initial oricare din produsele matriciale din
ecuatia de mai sus, iar apoi inmultim rezultatul inca o data (fie la
stanga, fie la dreapta, in functie de ordinea aleasa) cu matricea Hord.
De exemplu, daca alegem sa calculam initial
![]() , obtinem:
, obtinem:
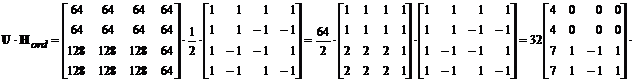
Acum inmultim rezultatul la stanga cu Hord si obtinem blocul transformat V:
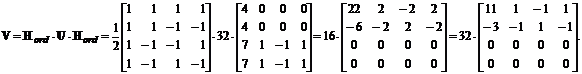
c) Demonstrarea conservarii energiei in domeniul transformat inseamna verificarea faptului ca energia blocului U se regaseste in totalitate in reprezentarea sa in domeniul transformat, adica in blocul V. In general, energia unui bloc de imagine se calculeaza ca suma patratelor valorilor luminantelor din bloc, iar energia blocului transformat - ca suma patratelor modulelor coeficientilor (identice cu patratele coeficientilor pentru transformari reale). Ca urmare, putem calcula energia EU in blocul de imagine original si energia EV in blocul de imagine reprezentat in domeniul transformat cu ecuatiile:
![]()
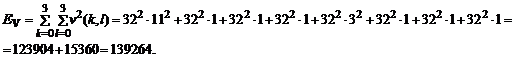
Se observa, din datele numerice obtinute, ca se verifica
relatia ![]() (ecuatia conservarii
energiei blocului in urma transformarii), ca urmare energia blocului se
conserva prin transformare.
(ecuatia conservarii
energiei blocului in urma transformarii), ca urmare energia blocului se
conserva prin transformare.
Compactarea energiei blocului in domeniul transformat, in comparatie cu distributia energiei blocului in domeniul original, poate fi estimata prin numarul de coeficienti nenuli din blocul transformat in care se "impacheteaza" energia imaginii. In blocul original, toti coeficientii sunt nenuli, dar in blocul transformat - doar 10 din cei 16 coeficienti sunt nenuli; ca urmare, energia in urma transformarii se impacheteaza in 10 din cei 16 coeficienti. Oricum compactarea energiei este mai slaba comparativ cu cazul blocului din problema 1, datorita specificului imaginii (in problema 1, blocul U continea o singura muchie verticala, care se "potrivea" perfect cu vectorul de baza de pe a doua linie/a doua coloana a matricii transformarii Hadamard, in timp ce in blocul din aceasta problema, avem forme ale liniilor 2 si 3 care necesita practic utilizarea tuturor vectorilor de baza, cu ponderi corespunzatoare, pentru aproximarea acestor forme de semnale dreptunghiulare, care prezinta tranzitii numai pe ultimul esantion). Avem deci prin transformare o compactare a energiei in 10/16 din coeficienti, adica in 62.5% din coeficienti - nu foarte eficienta.
a) Pentru blocul de imagine U din problema anterioara, proiectati o masca G 4×4] in domeniul coeficientilor transformarii Hadamard ordonate cu ajutorul careia sa se realizeze o filtrare a blocului, astfel incat in urma filtrarii si transformarii inverse a blocului filtrat in domeniul spatial, in blocul filtrat Uf[4×4], sa avem prezenta doar o singura muchie orizontala (sa dispara cu totul muchia verticala si coltul din bloc). Cum arata blocul refacut in domeniul spatial in urma filtrarii?
Filtrarea se va realiza prin operatia liniara de multiplicare intre coeficientii matricii G si coeficientii blocului transformat V[4×4], conducand la blocul filtrat in domeniul transformat Vf
![]()
unde:
![]() elementul de pe linia k
si coloana l din matricea Vf
elementul de pe linia k
si coloana l din matricea Vf
![]() elementul de pe linia k
si coloana l din matricea G
elementul de pe linia k
si coloana l din matricea G
![]() elementul de pe linia k
si coloana l din matricea V
elementul de pe linia k
si coloana l din matricea V
b) Care va fi efectul filtrarii blocului in domeniul transformatei Hadamard ordonate, folosind o masca de filtrare G[4×4] in domeniul coeficientilor transformarii Hadamard ordonate cu urmatorii coeficienti, aplicata conform ecuatiei liniare de mai sus?

Rezolvare:
a) Consideram ca avem calculata (conform rezolvarii din problema 3) matricea coeficientilor in domeniul transformatei Hadamard ordonate a blocului de imagine U, sub forma blocului V
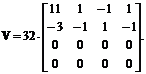
Cunoastem din teoria transformarilor bidimensionale unitare separabile (in particular, pentru transformata Hadamard ordonata) semnificatia corespondentei intre liniile, coloanele matricii coeficientilor in domeniul transformat si frecventele spatiale orizontala, respectiv verticala, pentru functii de baza dreptunghiulare:
coltul stanga sus al blocului transformat cu ajutorul transformarii Hadamard bidimensionale ordonate corespunde coeficientului de curent continuu (frecventelor zero pe orizontala si verticala) (pentru o imagine - coeficientul de curent continuu reprezinta luminanta medie a blocului);
indicele liniei blocului este o masura a frecventei spatiale verticale, iar indicele coloanei blocului - o masura a frecventei spatiale orizontale. Prima linie (linia 0) reprezinta frecventa spatiala verticala zero; ca urmare, mergand pe prima linie de la stanga la dreapta, avem coeficientii care reflecta prezenta unor tranzitii de tip dreptunghiular (salturi de luminanta) cu frecventa verticala nula si frecventa orizontala din ce in ce mai mare (mergand de la coloana 1 pana la coloana 3). Aceste salturi avand frecventa orizontala mare, reprezinta salturi de luminanta pe linie de pixeli (pe linii din U), dar neinsotite de salturi pe coloana (de frecvente verticala mare), deci vor corespunde muchiilor verticale din bloc. Prima coloana (coloana 0) reprezinta dimpotriva frecventa spatiala orizontala zero; ca urmare, mergand pe prima coloana de sus in jos, avem coeficientii care reflecta prezenta unor tranzitii de tip dreptunghiular (salturi de luminanta) cu frecventa orizontala nula si frecventa verticala din ce in ce mai mare (mergand de la linia 1 pana la linia 3). Aceste salturi avand frecventa verticala mare, reprezinta salturi de luminanta pe coloana de pixeli (pe coloanele din U), dar neinsotite de salturi pe linie (de frecventa orizontala mare), deci vor corespunde muchiilor orizontale din bloc. Coeficientii nenuli de pe linii si coloane oarecare (de pe o linie k si coloana l oarecare, k>0 si l>0) vor corespunde prezentei, intr-o pozitie spatiala din blocul de pixeli U, unor salturi bruste de luminanta atat pe linie, cat si pe coloana (adica, unor colturi), deoarece prezinta simultan o componenta de frecventa verticala si orizontala. Numarul de coeficienti nenuli, valoarea lor si pozitia lor pe linii si coloane va depinde atat de numarul de muchii orizontale, verticale si colturi, cat si de pozitia lor in blocul de pixeli. Ceea ce putem sti cu siguranta este ca:
pentru un bloc de pixeli care nu contine deloc tranzitii de luminanta (are luminanta perfect uniforma), vom avea un singur coeficient nenul in matricea coeficientilor transformatei sale Hadamard ordonate, in coltul stanga sus al matricii (pe linia 0 si coloana 0)
pentru un bloc de pixeli care contine doar muchii perfect orizontale (tranzitii de luminanta pe coloane perfect aliniate spatial - salturi bruste de luminanta la exact aceeasi linie din U pe toate coloanele), vom avea in matricea coeficientilor transformatei sale Hadamard ordonate, coeficienti nenuli doar pe prima coloana, toti coeficientii de pe celelalte coloane fiind nuli (0).
pentru un bloc de pixeli care contine doar muchii perfect verticale (tranzitii de luminanta pe linii perfect aliniate spatial - salturi bruste de luminanta la exact aceeasi coloana din U pe toate liniile), vom avea in matricea coeficientilor transformatei sale Hadamard ordonate, coeficienti nenuli doar pe prima linie, toti coeficientii de pe celelalte linii fiind nuli (0).
In alte situatii, ne putem astepta la coeficienti nenuli oriunde in matricea coeficientilor transformatei Hadamard ordonate a blocului.
Analizand matricea V a coeficientilor in domeniul transformatei Hadamard ordonate a blocului de imagine U de mai sus, comparativ cu distributia luminantelor din blocul U, observam ca:
avem un coeficient de curent continuu nenul (de asteptat de altfel, dat de media luminantelor din blocul de imagine U
avem un singur coeficient nenul pe prima coloana (coloana 0, corespunzatoare frecventelor verticale nenule si frecventei orizontale zero), de valoare -96; el trebuie sa corespunda muchiei orizontale de la mijlocul blocului, dintre primele doua si ultimele doua linii din bloc, muchie care se extinde insa doar pe primele trei coloane (deci nu este o muchie exclusiv orizontala prezenta in tot blocul), de unde si coeficientii nenuli care apar pe a doua linie si ultimele trei coloane din blocul V (date de coltul din imaginea U, localizat pe a treia linie si a treia coloana)
avem trei coeficienti nenuli pe prima linie (linia 0, corespunzatoare frecventelor orizontale nenule si frecventei verticale zero), de valori 32, -32 si respectiv 32; ei trebuie sa corespunda portiunii de muchie verticala de pe ultimele doua linii din blocul de pixeli U, dintre penultima si ultima coloana a blocului.
In conformitate cu aceasta analiza, daca dorim acum sa filtram blocul printr-o operatie de prelucrare a coeficientilor transformarii Hadamard ordonate (modificand astfel corespunzator prelucrarii si blocul de pixeli U), astfel incat in urma filtrarii si transformarii inverse a blocului filtrat in domeniul spatial, in blocul filtrat Uf[4×4], sa avem prezenta doar o singura muchie orizontala (sa dispara cu totul muchia verticala si coltul din bloc), inseamna ca va trebui sa retinem din coeficientii blocului V, doar pe cei responsabili de introducerea muchiei orizontale si sa setam toti ceilalti coeficienti la 0 (sa-i "stergem"); muchia orizontala se va "extinde" pe tot blocul de pixeli filtrati. Avem un singur coeficient in blocul V care reda prezenta muchiei orizontale, si anume, coeficientul de valoare -96 prezent pe prima coloana si a doua linie a blocului V. Ca urmare, masca de filtrare G[4×4] (care arata cu ce valori se inmultesc coeficientii transformarii Hadamard ordonate a blocului U pentru realizarea filtrarii) poate fi de forma:
 sau
sau 
dat fiind ca oricum, dintre toti coeficientii de pe prima coloana din blocul V, doar coeficientul de pe prima linie este nenul, deci celelalte valori ale G pe prima coloana nu au efect asupra filtrarii blocului.
Cu aceasta definire a coeficientilor mastii de filtrare, gasim valorile coeficientilor blocului filtrat in domeniul transformarii Hadamard bidimensionale cu expresia:
![]()
adica:
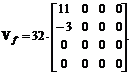
Blocul refacut in domeniul spatial in urma filtrarii, notat prin Uf[4×4], se determina prin aplicarea transformarii Hadamard ordonate inverse asupra blocului de coeficienti filtrat Vf
![]()
Cum matricea
transformarii Hadamard ordonate este
unitara, reala si simetrica (v. teorie, respectiv
demonstratie la problema 3), ![]() Ca urmare, formula de calcul a transformatei
Hadamard inverse bidimensionale se simplifica la forma:
Ca urmare, formula de calcul a transformatei
Hadamard inverse bidimensionale se simplifica la forma:
![]()
Inlocuind cu expresiile matricii Hord si matricii Vf, obtinem:
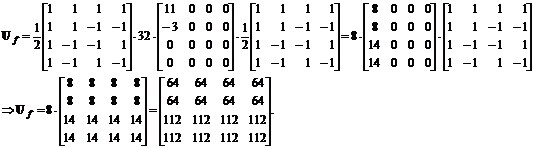
Observam ca primele doua linii din blocul Uf sunt identice cu primele doua linii din blocul original, inainte de filtrare, U. Apare intr-adevar in urma filtrarii in blocul Uf o singura muchie orizontala, disparand orice tranzitie de luminanta pe liniile blocului filtrat (orice muchie verticala sau colt). Observam deasemenea ca luminantele pe ultimele doua linii din blocul filtrat Uf sunt sub 128 (valoarea de luminanta de pe ultimele doua linii pe pozitia primelor trei coloane din blocul U), dar peste 64 (valoarea de luminanta de pe ultimele doua linii pe pozitia ultimei coloane din blocul U); la o examinare mai atenta, valoarea noii luminante pe oricare pozitie din ultimele doua linii din matricea filtrata este media luminantei pe fiecare din ultimele doua linii din blocul nefiltrat (corespunzator filtrarii trece jos pe directia frecventelor spatiale orizontale - filtrare care a fost echivalenta unei medieri spatiale pe aceasta directie): 112=(3∙128+64)/4.
b)
Efectul filtrarii blocului in domeniul
transformatei Hadamard ordonate, folosind masca de filtrare  in domeniul coeficientilor
transformarii Hadamard ordonate, poate fi estimat analizand
componenta acestei masti, in conformitate cu discutia de la
pct. a).
in domeniul coeficientilor
transformarii Hadamard ordonate, poate fi estimat analizand
componenta acestei masti, in conformitate cu discutia de la
pct. a).
Observam ca in masca G, toate elementele sunt zero cu exceptia celor de pe prima linie - doar de la a doua pana la ultima coloana, adica:
masca va "taia" componentele de frecventa verticala sau mixte verticala-orizontala;
masca va "taia" componenta continua (luminanta medie) din imagine, coeficientul de frecvente spatiale zero (de pe prima linie si prima coloana) avand ca factor de multiplicare in masca G o valoare nula;
masca lasa nemodificate doar componentele de frecventa orizontala pure (care corespund muchiilor strict verticale din blocul de imagine).
Ca urmare, efectul aplicarii mastii G cu elementele de mai sus asupra blocului de imagine este de filtrare trece sus pe directie strict orizontala. Dat fiind ca luminanta medie (descrisa de coeficientul de curent continuu) este setata la zero in urma filtrarii cu masca G, prin anularea coeficientului de curent continuu in urma filtrarii, ne asteptam ca in blocul filtrat, reprezentat in domeniul spatial, valorile rezultate in fiecare pozitie spatiala (pixel) sa nu fie luminante in domeniul , ci valori pozitive si negative, pentru a da per ansamblu o valoare medie nula. Acesta este motivul pentru care un bloc de imagine filtrat trece sus (in domeniul frecventa sau spatial) nu poate fi afisat pe ecran in forma in care rezulta prin filtrare, fiind necesara fie o translatie a valorilor (de obicei cu nivelul de gri mediu, 127 sau 128) care sa le aduca in domeniul de valori strict pozitive (cu limitarea lor la 255 daca depasesc in urma translatiei aceasta valoare), fie o reprezentare a valorilor blocului filtrat in modul (caz in care translatia nu mai este necesara), care permite afisarea, dar pierde bineinteles o parte din informatie (semnul) (fiind astfel utila pentru vizualizare, dar uneori insuficienta pentru prelucrari ulterioare complete).
Aplicand (cu operatia liniara descrisa la punctul a)) aceasta masca de filtrare G in domeniul transformatei Hadamard ordonate, obtinem coeficientii transformatei Hadamard bidimensionale corespunzatori blocului filtrat Vf
![]()
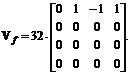
Reprezentarea blocului filtrat in domeniul spatial Uf[4×4] se obtine prin transformarea Hadamard bidimensionala ordonata inversa, data de ecuatia (v. pct. a)):
![]()
Inlocuind cu expresiile matricii Hord si matricii Vf, obtinem:
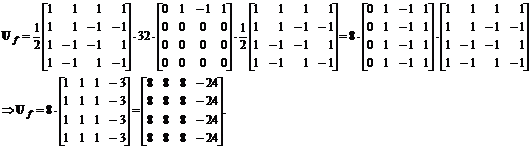
Asa cum era de asteptat, valoarea medie a blocului filtrat Uf este zero ((8∙12-4∙24)/16 =(96-96)/16=0), dat fiind ca filtrarea este strict trece sus; mai mult, filtrarea eliminand orice frecvente spatiale cu exceptia celor strict orizontale, avem prezenta in blocul filtrat reprezentat in domeniul spatial doar o muchie strict verticala (pe aceeasi pozitie ca si coloana pe care era prezenta si muchia verticala in blocul original U, nefiltrat, doar ca acum ea se extinde pe toata inaltimea blocului, fiind singura categorie de frecvente spatiale ramasa in imagine).
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |