
Convolutii si corelatii
Obiectivele lucrarii
1) Asimilarea functiilor MATLAB pentru realizarea convolutiilor, corelatiilor 1D si 2D;
Studiul algoritmilor pentru calculul convolutiilor si corelatiilor
3) Studiul interactiv al convolutiilor si transformatelor utilizand mediul DIDACTICIEL.
Desfasurarea lucrarii
Interpretarea polinomiala a convolutiei liniare si ciclice
Operatiile de convolutie liniara si ciclica, precum si de deconvolutie se pot interpreta prin prisma operatiilor cu polinoame. Sa consideram secventele 1D si polinoamele asociate de mai jos:
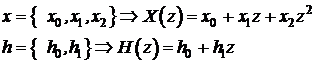
Conform
definitiei: 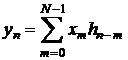 . Se obtine prin urmare:
. Se obtine prin urmare:
![]()
Aceiasi coeficienti
pot fi obtinuti ca urmare a produsului polinoamelor ![]() :
:
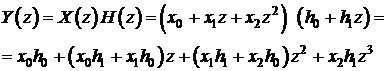
Functia
MATLAB conv pentru calculul convolutiilor
liniare 1D calculeaza de fapt acest produs. De exemplu, pentru a realiza
convolutia secventelor ![]() se utilizeaza:
se utilizeaza:
x=[1,2,3] ; h=[1,1] ; [y]=conv(x,h)
Deconvolutia poate fi realizata cu functia MATLAB deconv si poate fi vazuta ca rezultatul impartirii cu rest a polinoamelor Y si X.
[q,r]=deconv(y,x)
Si convolutia ciclica admite o interpretare polinomiala. Sa consideram secventele:
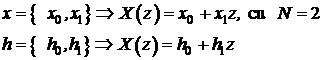
Conform
definitiei: 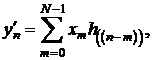 se obtine:
se obtine:
![]()
Acelasi
rezultat se obtine ca rest al operatiei polinomiale: ![]() , adica ca rest al impartirii polinomului
, adica ca rest al impartirii polinomului ![]() prin
prin ![]() .
.
Un exemplu de convolutie ciclica 1D este prezentat mai jos:
x=[1,2]; h=[3,4]; m=[1,0,-1];
[q,y]=deconv(fliplr(conv(x,h)),m)
Aceleasi consideratii sunt valabile si in cazul secventelor 2D. Astfel, in cazul convolutiei liniare:
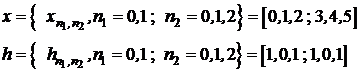
Modul de calcul
al primelor elemente ale secventei 2D ![]() este prezentat mai
jos:
este prezentat mai
jos:
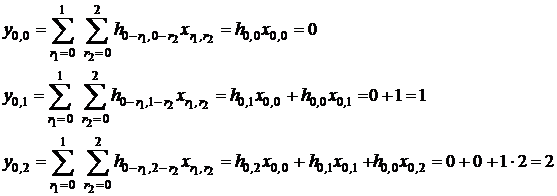
Rezultatul complet se obtine utilizand comenzile MATLAB:
x=[0,1,2;3,4,5] ; h=[1,0,1;1,0,1] ;
y=conv2(x,h)
Acelasi rezultat poate fi obtinut reprezentand convolutia ca produs de polinoame:
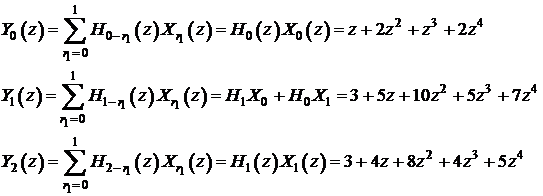
Reprezentand fiecare secventa 2D ca un polinom de doua variabile, se obtine:
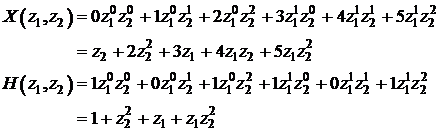
Se poate deci scrie convolutia 2D sub forma polinomulului de doua variabile:
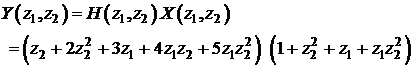
Teorema lui Plancherel
Pentru a verifica teorema lui Plancherel se poate considera urmatorul exemplu:
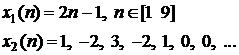
w = -pi:2*pi/255:pi;
x1 = [1 3 5 7 9 11 13 15 17];x2 = [1 -2 3 -2 1];
y = conv(x1,x2);h1 = freqz(x1, 1, w);
h2 = freqz(x2, 1, w);hp = h1.*h2;h3 = freqz(y,1,w);
subplot(2,2,1) ;plot(w/(2*pi),abs(hp));grid
title('Produsul spectrelor de amplitudine')
subplot(2,2,2) ;plot(w/(2*pi),abs(h3));grid
title('Spectrul de amplitudine a rezultatului convolutiei')
subplot(2,2,3) ;plot(w/(2*pi),angle(hp));grid
title('Suma spectrelor de faza')
subplot(2,2,4) ;plot(w/(2*pi),angle(h3));grid
title('Spectrul de faza a rezultatului convolutiei')
Calculul convolutiilor cu ajutorul transformatei Fourier
Sa se
calculeze convolutia ciclica a doua secvente, ![]() si
si ![]() , de aceeasi perioada
, de aceeasi perioada ![]() , utilizand
, utilizand ![]() .
.
x=[1,2]; h=[3,4];
X=fft(x);H=fft(h);Y=X.*H;
y=abs(ifft(Y))
Sa se utilizeze aceeasi metoda pentru a realiza convolutia ciclica 2D dintre secventele:
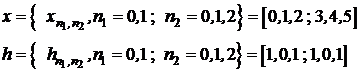
x=[1,2,3;4,5,6]; h=[1,0,1;1,0,1];
X=fft2(x); H=fft2(h);
Y=X.*H;
y=abs(ifft2(Y))
Mecanismul de calcul al convolutiei
Sa se
calculeze pas cu pas convolutia a doua secvente discrete.
Originea celor doua functii este presupusa la ![]() .
.
x=ones(3,1); h=exp(-[1:10]);
Ly=length(x)+length(h)-1;
lh=length(h);lx=length(x); y=zeros([Ly,1]);
xf=fliplr(x);
disp(['Apasati pe orice tasta pentru a calcula convolutia']);
for i=1:1:Ly
indlo=max(0,i-lx); indhi=min(i-1,lh-1);
for j=indlo:indhi
y(i)=h(j+1)*x(i-j)+y(i);
end
subplot(311);stem(-lx+i:1:i-1,xf);ylabel('x in oglinda');
lim1= max(lh,lx) ;lim2= min(min(min(x),min(h)),0) ;
lim3= max(max(x),max(h)) ;
axis([-lx,lim1,lim2,lim3]);
subplot(312);stem(0:1:lh-1,h);ylabel('h');
axis([-lx,lim1,lim2,lim3]);
subplot(313);stem(0:1:Ly-1,y);ylabel('y');
pause
end
Convolutia, corelatia si filtrajul adaptat
Sa se scrie un program care sa arate ca operatia de convolutie realizata de un filtru adaptat este echivalenta cu corelatia dintre semnalul cu care acesta este adaptat si semnalul de intrare.
Se va considera semnalul de intrare:
![]()
si filtrul adaptat caracterizat prin functia pondere:
![]()
h = [3 2 1 -2 1 0 -4 0 3];
x = [1 -2 3 -4 3 2 1];
xa = fliplr(h);
y1 = conv(h,x) ;
y2 = filter(h,1,[x zeros(1,length(x)+1)]);
y3 = xcorr(x,xa);
subplot(311);stem(y1); ylabel('Amplitudine');
title('Iesire obtinuta prin convolutie'); grid;
subplot(312);stem(y2); ylabel('Amplitudine');
title('Iesire obtinuta prin filtraj'); grid;
subplot(313);stem(y1)
xlabel('Index temporal n'); ylabel('Amplitudine');
title('Iesire obtinuta prin corelatie'); grid;
Studiul operatorilor de convolutie si corelatie utilizand mediul DIDACTICIEL
1) Se lanseaza DIDACTICIEL-ul prin introducerea comenzii:
didact
2) Se studiaza interactiv operatorii de convolutie si corelatie cu ajutorul meniurilor definite in:
Math Tools
Tema
Se dau secventele 1D:
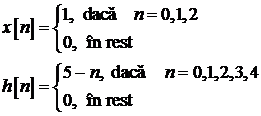
Calculati
analitic convolutia lor ciclica pentru ![]() si
verificati rezultatul in MATLAB.
si
verificati rezultatul in MATLAB.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |