se foloseste la rezolvarea sistemelor de n ecuatii liniare cu n necunoscute.
Se considera un sistem de n ecuatii liniare cu n necunoscute x1, x2, , xn, care poate fi scris astfel:
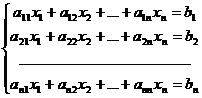
care poate fi reprezentata sub forma: Ax=b, unde A=(aij) n - matrice , x,b IRn - vectori, det A 0.
Daca vom completa matricea cu o coloana alcatuita din termenii liberi al sistemului, vom capata o matrice noua, care poarta denumirea de matrice extinsa a sistemului
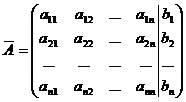 unde
coeficientii liberi bi se noteaza prin ain+1 (i=1,2,.n)
unde
coeficientii liberi bi se noteaza prin ain+1 (i=1,2,.n)
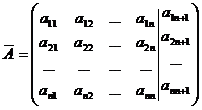
In memoria calculatorului matricea extinsa se pastreaza in forma unui tablou bidimensional de numere reale.
Calculul solutiei sistemului prin metoda Gauss se efectuiaza in doua etape:
Etapa mersului direct.
(eliminarea succesiva a necunoscutelor prin transformari echivalente a sistemului aducindu-l la o forma cu matricea superior triunghiulara).
Etapa mersului invers.
(se calculeaza necunoscutele)
Algoritmul etapei mersului direct
Pasul 1. Ca scop se pune eliminarea necunoscutei x1 din ecuatiile cu numerele
i = 2, ., n. Presupunem ca coeficientul a11 0. In caz contrar trebuie sa alegem din ecuatiile plasate mai jos acea ecuatie la care ai1 0, si sa schimbam cu locurile prima ecuatie si ecuatia i. La toti pasii care urmeaza aceasta operatie se repeta, in caz de necesitate.
Vom calcula ci1 = ai1/a11 (i = 2, 3, ., n) si vom scadea consecutiv din ecuatiile 2, 3, , n prima ecuatie inmultita respectiv la c21, c31, ., cn1. Aceste operatii transforma in zero coeficientii pe linga x1 in toate ecuatiile cu exceptia primei. Ca rezultat capatam un sistem echivalent de ecuatii
c11x1 + c12x2 + c13x3 + . + c1nxn - c1n+1= 0 ,
a22(1)x2 + a23(1)x3 + . + a2n(1)xn - a2n+1(1) = 0 ,
a32(1)x2 + a33(1)x3 + . + a3n(1)xn - a3n+1(1) = 0,
. . . . . . . . . . . . . . .
an2(1)x2 + an3(1)x3 + . + ann(1)xn - ann+1(1) = 0 .
in care aij(1) se calculeaza asa: aij(1) = aij − ci1a1j
Iteram procesul, eliminind necunoscutele xi din ecuatiile i+1, . ,n(i=2,.,n-1)
Vom descrie pasul k.
Pasul k. In conditia ca akk(k-1) 0 calculam cik = aik(k-1) / akk(k-1) (i = k + 1, ., n)
si scadem din ecuatiile (k + 1), ., n ecuatia k obtinuta la pasul precedent si inmultita respectiv la ck+1,k, ck+2,k, ., cnk.
Dupa pasul (n - 1) de eliminari obtinem urmatorul sistem de ecuatii:
a11x1 + a12x2 + a13x3 + . + a1nxn - a1n+1 = 0,
a22(1)x2 + a23(1)x3 + . + a2n(1)xn - a2n+1(1) = 0,
a33(2)x3 + . + a3n(2)xn - a3n+1(2) = 0,
. . . . . . . . . . . . . . . . . . . .
ann(n-1)xn - ann+1(n-1)
cu matricea extinsa A n-1) de coeficienti superior triunghiulara.
Algoritmul etapei inverse
Din ultima ecuatie a sistemului calculam xn. Substituim xn prin valoarea gasita in toate ecuatiile incepind cu a (n-1) pina la prima si calculam consecutiv xn-1, xn-2, ., x1. Necunoscutele se calculeaza dupa urmatoarele formule:
xn = ann+1(n-1) / ann(n-1),
xk = (ann+1(k-1) - ak,k+1(k-1)xk+1 - . - akn(k-1)xn) / akk(k-1), (k = n - 1, ., 1).
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |