Facultatea Cibernetica , Statistica si Informatica Economica
Modelul Kaldor
MODELUL KALDOR
Cadrul teoretic al acestui model a fost elaborat independent de diferiti economisti de renume : Jan Timbengen (Olanda), Henry Schultz (SUA), Umberto Ricci (Italia), Nicolas Kaldor (Anglia) s. a.
Modelul - cunoscut , dupa forma graficului, sub numele de "panza de paianjen" sau "cobweb " - este un model dinamic derivat din modelul static de echilibru .
Ipotezele introduse de Kaldor si ceilalti economisti pentru generalizarea dinamica a modelului static sunt :
Cererea depinde de preturile curente .
Oferta perioadei curente este dependenta de preturile perioadei precedente, atunci cand producatorii au decis asupra nivelului productiei, tinand cont de preturile pietei in momentul deciziei.
Piata asigura, prin mecanisme de reglare, nivelul pretului fiecarei perioade, in concordanta cu abaterea intre cerere si oferta (deci cu nivelul cererii excedentare ).
ĺn ipoteza de mai sus, modelul dinamic de formare a preturilor intr-o forma simplificata, cand dependenta dintre cerere , respectiv oferta si pret este liniara, este :
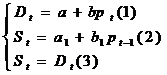 cu specificatiile ca, in
conditiile cererii
cu specificatiile ca, in
conditiile cererii
si ofertei normale, trebuie ca cererea marginala
sa fie negativa :![]() =
=![]() <0 si oferta marginala sa fie pozitiva
:
<0 si oferta marginala sa fie pozitiva
:![]() .
.
Deoarece ,
in conditiile echilibrului static ![]() deci pretul de
echilibru static este
deci pretul de
echilibru static este ![]()
![]() si are sens
economic daca
si are sens
economic daca ![]() , atunci, coeficientii
, atunci, coeficientii ![]() si
si ![]() care cuantifica
cererea si oferta incompresibila, trebuie sa verifice
conditia
care cuantifica
cererea si oferta incompresibila, trebuie sa verifice
conditia ![]() , adica in conditii normale cererea
incompresibila excedentara trebuie sa fie pozitiva, in
conditiile normale ale cererii si ofertei (deoarece in acest caz
, adica in conditii normale cererea
incompresibila excedentara trebuie sa fie pozitiva, in
conditiile normale ale cererii si ofertei (deoarece in acest caz ![]() ).
).
Modelul dinamic (1) - (3) da ecuatia de dinamica apreturilor :
(3)![]()
Traiectoria evolutiei preturilor este :
![]() unde
constanta
unde
constanta ![]() si
si ![]() este chiar expresia
pretului de echilibru analizat mai sus .
este chiar expresia
pretului de echilibru analizat mai sus .
Conditia
de stabilitate, daca initial pretul existent este departe de
pretul de echilibru, este ![]() . Atunci
. Atunci ![]() ,deci cand
,deci cand ![]() exista
conditiile mentinerii stabilitatii pretului .
exista
conditiile mentinerii stabilitatii pretului .
Daca ![]() , deci cand oferta marginala depaseste
cererea marginala - luate in valoare absoluta - atunci miscarea
pretului este exploziva.
, deci cand oferta marginala depaseste
cererea marginala - luate in valoare absoluta - atunci miscarea
pretului este exploziva.
Daca ![]() , miscarea este la limita de stabilitate, amplitudinea
variatiei lor fiind constanta.
, miscarea este la limita de stabilitate, amplitudinea
variatiei lor fiind constanta.
Consecinta: ĺn conditiile cererii si
ofertei normale, cum 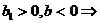 valoarea proprie
valoarea proprie ![]() .
.
Evolutia este deci
oscilanta, cu oscilatii improprii: pentru t=par se adauga la
pretul de echilibru expresia ![]() .
.
Ipoteza i2) nu reflecta comportamentul realist al producatorului, astfel ca va fi inlocuita cu:
i2') producatorul anticipeaza ca pretul
perioadei t va fi ![]() ,adica pretul asteptat a fi pe
piata in momentul desfacerii productiei.
,adica pretul asteptat a fi pe
piata in momentul desfacerii productiei.
Evident,
modelul Kaldor este un caz particular, in care ![]()
![]() si corespunde situatiei ca producatorii
nu anticipeaza evolutia preturilor .
si corespunde situatiei ca producatorii
nu anticipeaza evolutia preturilor .
Ecuatiile
(1) si (3) ale modelului preturilor raman aceleasi, dar
ecuatia ofertei (2) devine:![]()
![]() (2')
(2')
Exista
numeroase modele de fundamentare a pretului anticipat ![]() intrucat de calitatea
acestei estimari depinde intre altele calitatea deciziei agentului
economic, modelele cunoscute sunt fie deterministe , fie aleatoare.
Prezentam doua din modelele cele mai simple.
intrucat de calitatea
acestei estimari depinde intre altele calitatea deciziei agentului
economic, modelele cunoscute sunt fie deterministe , fie aleatoare.
Prezentam doua din modelele cele mai simple.
A) pretul anticipat este functie de nivelul pretului existent in perioada de baza si de abaterea intre acesta si un pret considerat ca normal de producatori in functie de evolutia cererii si ofertei , de utilitatea produsului, de nivelul concurentei si conjunctura pietei etc. Atunci pretul asteptat va fi :
![]() (6)
(6)
cu ![]() - pretul
considerat ca normal si c I
- pretul
considerat ca normal si c I ![]() este o constanta
care reflecta intarzierea ("lag") in atingerea pretului normal
.Astfel, daca
este o constanta
care reflecta intarzierea ("lag") in atingerea pretului normal
.Astfel, daca ![]() , deci in perioada urmatoare se ajunge la pretul
considerat normal ; daca
, deci in perioada urmatoare se ajunge la pretul
considerat normal ; daca ![]() , deci nu se atinge niciodata pretul "normal" (sau
altfel spus ,acesta va fi atins cu o intarziere infinita).
, deci nu se atinge niciodata pretul "normal" (sau
altfel spus ,acesta va fi atins cu o intarziere infinita).
Modelul dinamic de evolutie a preturilor , din ecuatiile (1),(2'),(3),(6) conduc la ecuatia :
![]() (7)
(7)
Daca pN = constant , se obtine traiectoria de miscare a pretului :
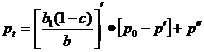 (8)
(8)
unde ![]() este nivelul de echilibru al pretului, ce rezulta
din (7):
este nivelul de echilibru al pretului, ce rezulta
din (7):
![]() (9)
(9)
Prima
componenta din ![]() comensureaza
efectul de multiplicare a cererii excedentare autonome
comensureaza
efectul de multiplicare a cererii excedentare autonome ![]() , multiplicatorul fiind
, multiplicatorul fiind ![]() si a doua componenta , efectul de multiplicare a
pretului "nominal" pN ,avand multiplicatorul
si a doua componenta , efectul de multiplicare a
pretului "nominal" pN ,avand multiplicatorul ![]() .
.
Din (8) se deduce conditia de stabilitate a pretului in jurul pretului de echilibru :
![]()
care reflecta o viteza mai mare de atingere a
echilibrului fata de modelul clasic "panza de paianjen".
Intr-adevar , deoarece ![]() , adica raportul
, adica raportul ![]() are in acest caz un domeniu mai larg de variatie pentru
a garanta stabilitatea :
are in acest caz un domeniu mai larg de variatie pentru
a garanta stabilitatea :
![]() (10)
(10)
in comparatie cu cazul studiat ![]()
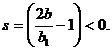
Programul matlab este creat pentru a ne arata traiectoriile acestui model in doua planuri cantitate - pret si timp - pret avand urmatorul program sursa:
clear;
fig=figure('menubar','none',
'numbertitle','off',
'color',[.50,.80,.90],
'name','Proiect CIBERNETICA');
mnMAIN1=uimenu(fig,'label','Introducerea datelor');
mnIS=uimenu(mnMAIN1,'label','Kaldor Simplu');
mnIDKS=uimenu(mnIS,'label','introduceti datele','callback','IDKS');
mnIR=uimenu(mnMAIN1,'label','Kaldor cu Anticipari Rationale');
mnIDKR=uimenu(mnIR,'label','introduceti datele','callback','IDKR');
mnMAIN=uimenu(fig,'label','Modelul Kaldor');
mnKS=uimenu(mnMAIN,'label','Kaldor Simplu ');
mnKSTP=uimenu(mnKS,'label','Grafic Timp Pret','callback','KSTP');
mnKSCP=uimenu(mnKS,'label','Grafic Cantitate Pret','callback','KSCP');
mnKR=uimenu(mnMAIN,'label','Kaldor cu Anticipari Rationale');
mnKRTP=uimenu(mnKR,'label','Grafic Timp Pret','callback','KRTP');
mnKRCP=uimenu(mnKR,'label','Grafic Cantitate Pret','callback','KRCP');
cu procedurile:
IDKS:
prompt = ;
title = 'parametrii modelului Kaldor Simplu';
p = inputdlg(prompt,title);
a=str2num(p);
b=str2num(p);
a1=str2num(p);
b1=str2num(p);
pzero=str2num(p);
eps=str2num(p);
IDKR:
prompt = ;
title = 'parametrii modelului Kaldor cu Anticipari Rationale';
p = inputdlg(prompt,title);
a=str2num(p);
b=str2num(p);
a1=str2num(p);
b1=str2num(p);
pzero=str2num(p);
eps=str2num(p);
pn=str2num(p);
c=str2num(p);
KSTP:
clear;
fid=fopen('KS.txt');
a=str2num(fgetl(fid));
b=str2num(fgetl(fid));
a1=str2num(fgetl(fid));
b1=str2num(fgetl(fid));
pzero=str2num(fgetl(fid));
eps=str2num(fgetl(fid));
fclose(fid);
p=(a-a1)/(b1-b);
% disp('pretul de echilibru static este:',p);
pt=pzero ;
c=pt-p ;
k=2 ;
while abs(pt-p)>eps
pt=c*((b1/b)^(k-1))+p ;
k=k+1;
end
x=0:1:k-2 ;
pn=1:1:k-1;
pn(1)=pzero;
k=2;
while(abs(pn(k-1)-p)>eps)
pn(k)=c*((b1/b)^(k-1))+p;
k=k+1;
end
plot(x,pn).
KSCP:
clear;
fid=fopen('KS.txt');
a=str2num(fgetl(fid));
b=str2num(fgetl(fid));
a1=str2num(fgetl(fid));
b1=str2num(fgetl(fid));
pzero=str2num(fgetl(fid));
eps=str2num(fgetl(fid));
fclose(fid);
p=(a-a1)/(b1-b);
% disp('pretul de echilibru static este:',p);
pt=pzero ;
c=pt-p ;
k=2 ;
while abs(pt-p)>eps
pt=c*((b1/b)^(k-1))+p ;
k=k+1;
end
x=0:1:k-2 ;
pn=1:1:k-1;
pn(1)=pzero;
g=1:1:2*(k-1) ;
g(1)=a+b*pzero;
g(2)=a1+b1*pzero ;
pf=1:1:2*(k-1) ;
pf(1)=pzero ;
pf(2)=pzero;
k=2;
while(abs(pf(2*k-2)-p)>eps)
pf(2*k-1)=c*((b1/b)^(k-1))+p; , pf(2*k)=c*((b1/b)^(k-1))+p;
g(2*k-1)=a+b*(c*((b1/b)^(k-1))+p);
g(2*k)=a1+b1*(c*((b1/b)^(k-1))+p);
k=k+1;
end
plot(g,pf);
KRTP:
clear;
fid=fopen('KR.txt');
a=str2num(fgetl(fid));
b=str2num(fgetl(fid));
a1=str2num(fgetl(fid));
b1=str2num(fgetl(fid));
pzero=str2num(fgetl(fid));
eps=str2num(fgetl(fid));
pN=str2num(fgetl(fid));
c=str2num(fgetl(fid));
fclose(fid);
pt=pzero ;
pSt=(a1-a)/(b-b1+b1*c)+b1*c*pN/(b-b1+b1*c) ;
k=2;
while abs(pt-pSt)>eps
pt=((b1*(1-c)/b)^(k-1))*(pzero-pN)+pSt;
k=k+1;
end
x=0:1:k-2;
pn=1:1:k-1;
pn(1)=pzero;
k=2;
while abs(pn(k-1)-pSt)>eps
pn(k)=((b1*(1-c)/b)^(k-1))*(pzero-pN)+pSt;
x(k-1)=k-2;
k=k+1;
end
x(k-1)=(k-2);
plot(x,pn) ;
KRCP:
clear;
fid=fopen('KR.txt');
a=str2num(fgetl(fid));
b=str2num(fgetl(fid));
a1=str2num(fgetl(fid));
b1=str2num(fgetl(fid));
pzero=str2num(fgetl(fid));
eps=str2num(fgetl(fid));
pN=str2num(fgetl(fid));
c=str2num(fgetl(fid));
fclose(fid);
pt=pzero ;, pSt=(a1-a)/(b-b1+b1*c)+b1*c*pN/(b-b1+b1*c) ;, k=2;
while abs(pt-pSt)>eps
pt=((b1*(1-c)/b)^(k-1))*(pzero-pN)+pSt; ,k=k+1;
end
x=0:1:k-2 ;, pn=1:1:k-1;
pn(1)=pzero;
g=1:1:2*(k-1); , g(1)=a+b*pzero; , g(2)=a1+b1*pzero;
f=1:1:2*(k-1); , pf(1)=pzero; , pf(2)=pzero;
k=2;
while(abs(pf(2*k-2)-pSt)>eps)
pf(2*k-1)=((b1*(1-c)/b)^(k-1))*(pzero-pN)+pSt; , pf(2*k) = pf(2*k-1);
g(2*k-1)=a+b * pf(2*k); , g(2*k) =a1+b1*pf(2*k); , k=k+1;
end
plot(g,pf);
Datele pot fi introduse de la tastatura sau pot fi luate dintr-un fisier de tip text existent in program KS.txt si KR.txt.
Pentru modelul Kaldor simplu.
Pentru valorile a=740, b=-8, a1=20, b1=6 cu un pret initial de 80 u.m. si un interval de timp de 0.5 ani avem pretul de echilibru pe=51.43 si traiectpria:
Pt = 28.57(-0.75)t + 51.43
Observam ca suntem in cazul unei valori de echilibru stabile iar traiectoria pretului este amortizata graficul fiind prezentat in Matlab.
In cazul modelului cu anticipari rationale introducem pretul normal pn=50 si intarzierez de c=0.65 si avem:
Pe=52 u.m. si este un punct de echilibru stabil cu o traiectorie amortizata cum se poate vedea si din grafic.
Bibliografie
Bazele Ciberneticii Economice - Aplicatii micro si macro economice realizate in mediul Matlab , autori Liliana Spircu si Angela Galupa editura A.S.E., Bucuresti 2002
Modele dinamice ale economiei de piata - Studii de caz, Partea II, autori Oprescu Gheorghe, Andrei Anca, Marin Dumitru, Scarlat Emil, Tiganescu Eugen, Editura F.F. Press 1996
Modelul venituri-cheltuieli Hicks
Hicks expune acest model cu ajutorul diagramei IS-LM in care reprezinta esenta economiei keynesiene.Acest model al lui Keynes imaginat de Hicks poate fi reprezentat cu ajutorul a cinci ecuatii:
Functia venitului: Y = C(Y, r) + I(Y, r) ; (a)
Cererea balantei reale: Dn = L(Y, R) ; (b)
Functia de productie agregat: Y= f(N) cu
f'(N) > 0 si f"(N) < 0 ; (c)
Cererea de
forta de munca: f'(N) = F ![]() ; (d)
; (d)
Oferta de munca: N=
N ![]() ; (e)
; (e)
cand w ≥ w'.
Y se refera la venitul banesc total, C reprezinta acum consumul real. Forta de munca este singurul factor variabil de productie, iar schema cererii fortei de munca este data de prima derivata a functiei de productie agregat. Cererea si oferta de forta de munca sunt functii ale nivelului salariului "real", iar toate ecuatiile sunt functii ale valorilor "reale"; conditia
w ≥ w' va fi explicata in cursul prezentarii ideii.
Intregul model este
reprezentat in Fig.1, unde ![]() ,Ŷ,
,Ŷ,
![]() etc.
se refera la valorile variabilelor in conditiile deplinei
angajari a fortei de munca. Incepand cu ecuatia (c),
functia de productie agregat apare in cadranul IV. Cadranul III
reda ecuatiile (d) si (e), care impreuna determina
nivelul angajarii si nivelul salariului real la ocuparea totala
a locurilor de munca. Cadranul II ne ofera raportul dintre rata
dobanzii si rata salariului. Figura din cadranul I reprezinta
diagrama Hicks a echilibrului monetar din sistemul keynesian. Curba IS
din cadranul I reprezinta ecuatia (a) si arata
corelatia dintre rata dobanzii si nivelul venitului la echilibru,
care este determinata de egalitatea dintre economia planificata
si investitia planificata. Considerand oferta de bani ca
variabila exogena determinata de autoritatile
monetare, ecuatia (b) din cadranul I este reprezentata de
curba LM si exprima relatia de echilibru intre cererea
si oferta de bani la nivelul pretului care domina. Esenta
sistemului keynesian se bazeaza pe aceste doua scheme.
etc.
se refera la valorile variabilelor in conditiile deplinei
angajari a fortei de munca. Incepand cu ecuatia (c),
functia de productie agregat apare in cadranul IV. Cadranul III
reda ecuatiile (d) si (e), care impreuna determina
nivelul angajarii si nivelul salariului real la ocuparea totala
a locurilor de munca. Cadranul II ne ofera raportul dintre rata
dobanzii si rata salariului. Figura din cadranul I reprezinta
diagrama Hicks a echilibrului monetar din sistemul keynesian. Curba IS
din cadranul I reprezinta ecuatia (a) si arata
corelatia dintre rata dobanzii si nivelul venitului la echilibru,
care este determinata de egalitatea dintre economia planificata
si investitia planificata. Considerand oferta de bani ca
variabila exogena determinata de autoritatile
monetare, ecuatia (b) din cadranul I este reprezentata de
curba LM si exprima relatia de echilibru intre cererea
si oferta de bani la nivelul pretului care domina. Esenta
sistemului keynesian se bazeaza pe aceste doua scheme.
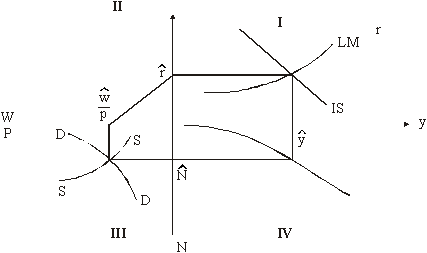
Fig. 1
In concordanta cu functia venitului (a), economia ca si investitia este o functie atat de Y cat si de r. Cu toate acestea, insusi Keynes a considerat economia ca fiind numai o functie de venit, iar investitia numai o functie a ratei dobanzii. Forma cea mai generala a functiei venitului la concluziile lui Keynes dovedind ca economia raspunde mai usor la variatiile venitului decat la cele ale ratei dobanzii; ideea opusa acesteia este valabila pentru investitii. Functia de investitii se prezinta ca o panta foarte inclinata in raport cu r in partea stanga sus si putin inclinata in raport cu Y in partea dreapta jos (Fig.2).
Cumulam la I functia de consum, descrisa ca o legatura liniara, de forma C = a + bY, in care a si b, sunt considerate pozitive. Functia economiei este determinata pe seama functiei de consum exprimata pe linia de 45°, care reprezinta functia ofertei agregat la Keynes. C + I reprezinta functia cererii agregat, iar intersectia celor doua functii Ye, reprezinta nivelul de echilibru al venitului.
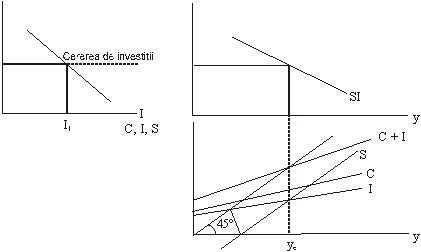
Fig. 2
Rata dobanzii fiind data, exista un anumit nivel de venit care va face ca economiile planificate sa fie egale cu investitiile planificate. Asadar, curba IS a lui Hicks reprezinta locul tuturor combinatiilor posibile ale lui r si Y care satisfac egalitatea dintre economiile si investitiile planificate.
Atunci cand rata dobanzii este inalta, investitia este mica ca si venitul, consecinta a multiplicatorului; considerand venitul mic, economia este mica. Nivelele ridicate ale venitului determina nivele ridicate ale economiei; rata dobanzii trebuie sa fie redusa pentru a produce o cantitate echivalenta de investitii.
Keynes a definit curba cererii de bani Dn=L1(Y)+L2(r), unde L1(Y) reprezinta cererea de tranzactii si balantele de siguranta, iar L2(r) reprezinta cererea de balante speculative. O rata inalta a dobanzii descurajeaza detinerile cash si incurajeaza detinerea de actiuni, nu numai datorita costului de oportunitate inalt al depozitelor cach, ci si datorita riscului neglijabil al pierderilor de capital la o viitoare crestere a ratei dobanzii sau la o viitoare scadere a preturilor actiunilor. Declinul ratei dobanzii mareste riscul pierderii de capital sub forma de actiuni si incurajeaza transformarea actiunilor in bani; la rate foarte scazute ale dobanzii si preturi inalte ale actiunilor, fiecare va astepta o marire a ratei dobanzii si va prefera, asadar, sa pastreze bani cash. Aceasta este esenta cererii speculative de bani in opinia lui Keynes.
Luand in considerare oferta de bani, functia keynesiana a cererii de bani impune ca echilibrul monetar sa implice o relatie stransa intre Y si r (Fig.3a). Tinand seama de stocul de bani si nivelul pretului, putem determina curba LM, care arata toate combinatiile posibile intre r si Y, care incurajeaza pastrarea stocului de bani existent (FIG.3b). Nivelurile veniturilor in crestere sunt asociate cu rate mai inalte ale dobanzii la fiecare nivel al pretului, intrucat pe masura ce venitul se mareste, tranzactiile si cererea de bani de siguranta sporesc, lasand o parte mai mica din oferta fixa reala de bani sa satisfaca cererea speculativa de balante goale; deci rata dobanzii trebuie sa creasca pentru a acoperi cererea speculativa.
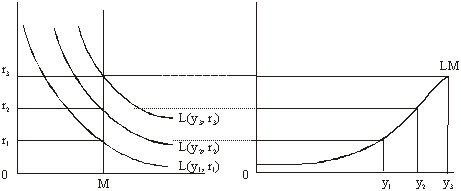
Fig. 3a Fig. 3b
|
Fig. 4 |
Punctul de intersectie al curbelor IS si LM (Fig.4) satisface dubla conditie a echilibrului monetar: economiile planificate egaleaza investitiile planificate si, in plus, cantitatea dorita de bani este egala cu oferta actuala de bani. Atat timp cat curba IS taie curba LM deasupra, acest punct de echilibru este stabil. Deplasarea la dreapta spre curba LM se datoreaza fie cresterii ofertei de bani, fie modificarii in jos a schemei preferintei lichiditatii, fie datorita unei scaderi a preturilor. Datorita naturii cererii speculative de bani, curba LM devine in mod crescator elastica la rate mai reduse ale dobanzii. Astfel sporurile egale ale stocului de bani vor conduce la reduceri succesive mai mici ale lui r si la cresteri succesive mai mari ale lui Y.
|
Fig. 5 |
Deplasarea spre dreapta a curbei IS reflecta fie o miscare in sus a functiei cererii de investitii, fie o modificare in jos a functiei economiilor (Fig.5). Inclinatia trebuie redusa pentru a salva cresterile IS cu o cantitate uniforma de-a lungul intregii sale lungimi. Acest lucru va mari in mod moderat pe Y si substantial pe r, daca curba LM este inelastica; daca curba LM este elastica, Y va creste substantial si r moderat. Deci: o inclinatie redusa pentru a salva sporul de venituri la o cerere crescuta de bunuri de consum, conduce la o crestere ulteriora a consumului si investitiilor pe calea multiplicatorului. O cantitate mai mare de bani este stransa pe seama tranzactiilor si balantelor de siguranta, deviind fondurile din balantele speculative prin cresterea ratei dobanzii.
Esenta ideii keynesiene este posibilitatea "echilibrului somajului": demonstratia ca nu exista nici un mecanism care sa garanteze ocuparea deplina a locurilor de munca intr-o economie concurentiala.
Se constata ca:
1) cererea de forta de munca si nivelul angajarilor sunt determinate de salariile reale, nu de salariile banesti, exact asa cum au remarcat economistii neoclasici;
2) reducere a salariilor banesti este totodata urmata de o reducere echivalenta a salariilor reale, cat timp preturile sunt determinate competitiv de costurile primare marginale, care pe o durata scurta de timp sunt formate in totalitate din costurile fortei de munca;
3) cat timp consumul real este o functie unica a venitului real si cat timp tendinta marginala spre consum a muncitorilor este mai mica decat unitatea, muncitorii vor cheltui mai putin.
Notatiile folosite in tabel au urmatorul continut:
S = economii; Y = productie; I = investitie; M = oferta de moneda; L = cererea de moneda; p = pretul bunurilor; N = volumul ocuparii; w = productivitatea marginala a muncii; Ns = numarul salariatiilor ocupati; ND = volumul cererii de muncitori; w/p=nivelul salariului real; i = rata dobanzii.
Program sursa:
disp('Introduceti parametrii:');
s=input('Propensiunea spre consum s= ');
beta=input('Coeficientul de accelerare beta= ');
y0=input('Introduceti valoarea initiala de venit y0=');
y1=input('Introduceti valoarea initiala de venit y1=');
G0=input('Introduceti valoarea initiala a chelt. guvernam. G0=');
r=input('Introduceti ritmul de crestere al chelt. guvernam. r=');
A1=[s+beta -beta;1 0];
[V,D]=eig(A1);
c=(G0*(1+r)^2)/((1+r)^2-(s+beta)*(1+r)+beta);
if (imag(D(1,1))~=0)
ro=abs(D(1,1));
teta=acos(real(D(1,1))/ro);
c1=(y0*D(2,2)-y1)/(D(2,2)-D(1,1));
c2=(-y0*D(1,1)+y1)/(D(2,2)-D(1,1));
for t=0:1:10
Timp(t+1)=t+1;
Venit(t+1)=2*abs(c1)*ro^t*cos(acos(real(c1)/abs(c1))+teta*t)+c*(1+r)^t;
Consum(t+1)=s*2*abs(c1)*ro^(t-1)*cos(acos(real(c1)/abs(c1))+teta*(t-1))+c*(1+r)^(t-1);
end
if (ro<1)
disp('Traiectorie oscilanta periodica amortizata');
else
disp('Traiectorie oscilanta periodica exploziva');
end
else
if (D(1,1)==D(2,2))
ro=0;
teta=0;
c1=y0;
c2=(y1-y0*D(1,1))/D(1,1);
for t=0:1:10
Timp(t+1)=t+1;
if (D(1,1)~=0)
Venit(t+1)=c1*D(1,1)^t+c2*t*D(1,1)^t+c*(1+r)^t;
Consum(t+1)=s*c1*D(1,1)^(t-1)+c2*(t-1)*D(1,1)^(t-1)+c*(1+r)^(t-1);
else
Venit(t+1)=0;
Consum(t+1)=0;
end
end
if (abs(D(1,1))<1)
disp('Traiectorie amortizata');
else
disp('Traiectorie exploziva');
end
else
ro=0;
teta=0;
c1=(y0*D(2,2)-y1)/(D(2,2)-D(1,1));
c2=(-y0*D(1,1)+y1)/(D(2,2)-D(1,1));
for t=0:1:10
Timp(t+1)=t+1;
Venit(t+1)=c1*D(1,1)^t+c2*D(2,2)^t+c*(1+r)^t;
Consum(t+1)=s*c1*D(1,1)^(t-1)+c2*D(1,1)^(t-1)+c*(1+r)^(t-1);
end
if ((abs(D(1,1))<1)&(abs(D(2,2))<1))
disp('Traiectorie amortizata');
end
if ((abs(D(1,1))>1)|(abs(D(2,2))>1))
disp('Traiectorie exploziva');
end
end
end
figure(1);
plot(Timp,Venit,'r-*');
title('TRAIECTORIA VENITULUI ');
legend('Venit');
hold on;
figure(2);
plot(Timp,Consum,'r-*');
title('TRAIECTORIA CONSUMULUI ');
legend('Consum');
hold on;
figure(3);
plot3(Timp,Venit,Consum,'r-*');
title('TRAIECTORIA VENIT-CONSUM ');
legend('Venit-Consum');
hold on;
 Bibliografie
Bibliografie
Bazele Ciberneticii Economice - Aplicatii micro si macro economice realizate in mediul Matlab , autori Liliana Spircu si Angela Galupa editura A.S.E., Bucuresti 2002
 2. www.unibuc.ro
2. www.unibuc.ro
Modelul venituri-cheltuieli Hicks
Hicks expune acest model cu ajutorul diagramei IS-LM in care reprezinta esenta economiei keynesiene.Acest model al lui Keynes imaginat de Hicks poate fi reprezentat cu ajutorul a cinci ecuatii:
Functia venitului: Y = C(Y, r) + I(Y, r) ; (a)
Cererea balantei reale: Dn = L(Y, R) ; (b)
Functia de productie agregat: Y= f(N) cu
f'(N) > 0 si f"(N) < 0 ; (c)
Cererea de
forta de munca: f'(N) = F ![]() ; (d)
; (d)
Oferta de munca: N=
N ![]() ; (e)
; (e)
cand w ≥ w'.
Y se refera la venitul banesc total, C reprezinta acum consumul real. Forta de munca este singurul factor variabil de productie, iar schema cererii fortei de munca este data de prima derivata a functiei de productie agregat. Cererea si oferta de forta de munca sunt functii ale nivelului salariului "real", iar toate ecuatiile sunt functii ale valorilor "reale"; conditia
w ≥ w' va fi explicata in cursul prezentarii ideii.
Intregul model este
reprezentat in Fig.1, unde ![]() ,Ŷ,
,Ŷ,
![]() etc.
se refera la valorile variabilelor in conditiile deplinei
angajari a fortei de munca. Incepand cu ecuatia (c),
functia de productie agregat apare in cadranul IV. Cadranul III
reda ecuatiile (d) si (e), care impreuna determina
nivelul angajarii si nivelul salariului real la ocuparea totala
a locurilor de munca. Cadranul II ne ofera raportul dintre rata dobanzii
si rata salariului. Figura din cadranul I reprezinta diagrama Hicks
a echilibrului monetar din sistemul keynesian. Curba IS din cadranul I
reprezinta ecuatia (a) si arata corelatia dintre rata
dobanzii si nivelul venitului la echilibru, care este determinata de
egalitatea dintre economia planificata si investitia
planificata. Considerand oferta de bani ca variabila exogena
determinata de autoritatile monetare, ecuatia (b) din
cadranul I este reprezentata de curba LM si
exprima relatia de echilibru intre cererea si oferta de bani la
nivelul pretului care domina. Esenta sistemului keynesian se
bazeaza pe aceste doua scheme.
etc.
se refera la valorile variabilelor in conditiile deplinei
angajari a fortei de munca. Incepand cu ecuatia (c),
functia de productie agregat apare in cadranul IV. Cadranul III
reda ecuatiile (d) si (e), care impreuna determina
nivelul angajarii si nivelul salariului real la ocuparea totala
a locurilor de munca. Cadranul II ne ofera raportul dintre rata dobanzii
si rata salariului. Figura din cadranul I reprezinta diagrama Hicks
a echilibrului monetar din sistemul keynesian. Curba IS din cadranul I
reprezinta ecuatia (a) si arata corelatia dintre rata
dobanzii si nivelul venitului la echilibru, care este determinata de
egalitatea dintre economia planificata si investitia
planificata. Considerand oferta de bani ca variabila exogena
determinata de autoritatile monetare, ecuatia (b) din
cadranul I este reprezentata de curba LM si
exprima relatia de echilibru intre cererea si oferta de bani la
nivelul pretului care domina. Esenta sistemului keynesian se
bazeaza pe aceste doua scheme.

Fig. 1
In concordanta cu functia venitului (a), economia ca si investitia este o functie atat de Y cat si de r. Cu toate acestea, insusi Keynes a considerat economia ca fiind numai o functie de venit, iar investitia numai o functie a ratei dobanzii. Forma cea mai generala a functiei venitului la concluziile lui Keynes dovedind ca economia raspunde mai usor la variatiile venitului decat la cele ale ratei dobanzii; ideea opusa acesteia este valabila pentru investitii. Functia de investitii se prezinta ca o panta foarte inclinata in raport cu r in partea stanga sus si putin inclinata in raport cu Y in partea dreapta jos (Fig.2).
Cumulam la I functia de consum, descrisa ca o legatura liniara, de forma C = a + bY, in care a si b, sunt considerate pozitive. Functia economiei este determinata pe seama functiei de consum exprimata pe linia de 45°, care reprezinta functia ofertei agregat la Keynes. C + I reprezinta functia cererii agregat, iar intersectia celor doua functii Ye, reprezinta nivelul de echilibru al venitului.

Fig. 2
Rata dobanzii fiind data, exista un anumit nivel de venit care va face ca economiile planificate sa fie egale cu investitiile planificate. Asadar, curba IS a lui Hicks reprezinta locul tuturor combinatiilor posibile ale lui r si Y care satisfac egalitatea dintre economiile si investitiile planificate.
Atunci cand rata dobanzii este inalta, investitia este mica ca si venitul, consecinta a multiplicatorului; considerand venitul mic, economia este mica. Nivelele ridicate ale venitului determina nivele ridicate ale economiei; rata dobanzii trebuie sa fie redusa pentru a produce o cantitate echivalenta de investitii.
Keynes a definit curba cererii de bani Dn=L1(Y)+L2(r), unde L1(Y) reprezinta cererea de tranzactii si balantele de siguranta, iar L2(r) reprezinta cererea de balante speculative. O rata inalta a dobanzii descurajeaza detinerile cash si incurajeaza detinerea de actiuni, nu numai datorita costului de oportunitate inalt al depozitelor cach, ci si datorita riscului neglijabil al pierderilor de capital la o viitoare crestere a ratei dobanzii sau la o viitoare scadere a preturilor actiunilor. Declinul ratei dobanzii mareste riscul pierderii de capital sub forma de actiuni si incurajeaza transformarea actiunilor in bani; la rate foarte scazute ale dobanzii si preturi inalte ale actiunilor, fiecare va astepta o marire a ratei dobanzii si va prefera, asadar, sa pastreze bani cash. Aceasta este esenta cererii speculative de bani in opinia lui Keynes.
Luand in considerare oferta de bani, functia keynesiana a cererii de bani impune ca echilibrul monetar sa implice o relatie stransa intre Y si r (Fig.3a). Tinand seama de stocul de bani si nivelul pretului, putem determina curba LM, care arata toate combinatiile posibile intre r si Y, care incurajeaza pastrarea stocului de bani existent (FIG.3b). Nivelurile veniturilor in crestere sunt asociate cu rate mai inalte ale dobanzii la fiecare nivel al pretului, intrucat pe masura ce venitul se mareste, tranzactiile si cererea de bani de siguranta sporesc, lasand o parte mai mica din oferta fixa reala de bani sa satisfaca cererea speculativa de balante goale; deci rata dobanzii trebuie sa creasca pentru a acoperi cererea speculativa.
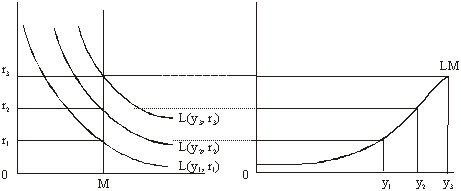
Fig. 3a Fig. 3b
|
Fig. 4 |
Punctul de intersectie al curbelor IS si LM (Fig.4) satisface dubla conditie a echilibrului monetar: economiile planificate egaleaza investitiile planificate si, in plus, cantitatea dorita de bani este egala cu oferta actuala de bani. Atat timp cat curba IS taie curba LM deasupra, acest punct de echilibru este stabil. Deplasarea la dreapta spre curba LM se datoreaza fie cresterii ofertei de bani, fie modificarii in jos a schemei preferintei lichiditatii, fie datorita unei scaderi a preturilor. Datorita naturii cererii speculative de bani, curba LM devine in mod crescator elastica la rate mai reduse ale dobanzii. Astfel sporurile egale ale stocului de bani vor conduce la reduceri succesive mai mici ale lui r si la cresteri succesive mai mari ale lui Y.
|
Fig. 5 |
Deplasarea spre dreapta a curbei IS reflecta fie o miscare in sus a functiei cererii de investitii, fie o modificare in jos a functiei economiilor (Fig.5). Inclinatia trebuie redusa pentru a salva cresterile IS cu o cantitate uniforma de-a lungul intregii sale lungimi. Acest lucru va mari in mod moderat pe Y si substantial pe r, daca curba LM este inelastica; daca curba LM este elastica, Y va creste substantial si r moderat. Deci: o inclinatie redusa pentru a salva sporul de venituri la o cerere crescuta de bunuri de consum, conduce la o crestere ulteriora a consumului si investitiilor pe calea multiplicatorului. O cantitate mai mare de bani este stransa pe seama tranzactiilor si balantelor de siguranta, deviind fondurile din balantele speculative prin cresterea ratei dobanzii.
Esenta ideii keynesiene este posibilitatea "echilibrului somajului": demonstratia ca nu exista nici un mecanism care sa garanteze ocuparea deplina a locurilor de munca intr-o economie concurentiala.
Se constata ca:
1) cererea de forta de munca si nivelul angajarilor sunt determinate de salariile reale, nu de salariile banesti, exact asa cum au remarcat economistii neoclasici;
2) reducere a salariilor banesti este totodata urmata de o reducere echivalenta a salariilor reale, cat timp preturile sunt determinate competitiv de costurile primare marginale, care pe o durata scurta de timp sunt formate in totalitate din costurile fortei de munca;
3) cat timp consumul real este o functie unica a venitului real si cat timp tendinta marginala spre consum a muncitorilor este mai mica decat unitatea, muncitorii vor cheltui mai putin.
Notatiile folosite in tabel au urmatorul continut:
S = economii; Y = productie; I = investitie; M = oferta de moneda; L = cererea de moneda; p = pretul bunurilor; N = volumul ocuparii; w = productivitatea marginala a muncii; Ns = numarul salariatiilor ocupati; ND = volumul cererii de muncitori; w/p=nivelul salariului real; i = rata dobanzii.
Program sursa:
disp('Introduceti parametrii:');
s=input('Propensiunea spre consum s= ');
beta=input('Coeficientul de accelerare beta= ');
y0=input('Introduceti valoarea initiala de venit y0=');
y1=input('Introduceti valoarea initiala de venit y1=');
G0=input('Introduceti valoarea initiala a chelt. guvernam. G0=');
r=input('Introduceti ritmul de crestere al chelt. guvernam. r=');
A1=[s+beta -beta;1 0];
[V,D]=eig(A1);
c=(G0*(1+r)^2)/((1+r)^2-(s+beta)*(1+r)+beta);
if (imag(D(1,1))~=0)
ro=abs(D(1,1));
teta=acos(real(D(1,1))/ro);
c1=(y0*D(2,2)-y1)/(D(2,2)-D(1,1));
c2=(-y0*D(1,1)+y1)/(D(2,2)-D(1,1));
for t=0:1:10
Timp(t+1)=t+1;
Venit(t+1)=2*abs(c1)*ro^t*cos(acos(real(c1)/abs(c1))+teta*t)+c*(1+r)^t;
Consum(t+1)=s*2*abs(c1)*ro^(t-1)*cos(acos(real(c1)/abs(c1))+teta*(t-1))+c*(1+r)^(t-1);
end
if (ro<1)
disp('Traiectorie oscilanta periodica amortizata');
else
disp('Traiectorie oscilanta periodica exploziva');
end
else
if (D(1,1)==D(2,2))
ro=0;
teta=0;
c1=y0;
c2=(y1-y0*D(1,1))/D(1,1);
for t=0:1:10
Timp(t+1)=t+1;
if (D(1,1)~=0)
Venit(t+1)=c1*D(1,1)^t+c2*t*D(1,1)^t+c*(1+r)^t;
Consum(t+1)=s*c1*D(1,1)^(t-1)+c2*(t-1)*D(1,1)^(t-1)+c*(1+r)^(t-1);
else
Venit(t+1)=0;
Consum(t+1)=0;
end
end
if (abs(D(1,1))<1)
disp('Traiectorie amortizata');
else
disp('Traiectorie exploziva');
end
else
ro=0;
teta=0;
c1=(y0*D(2,2)-y1)/(D(2,2)-D(1,1));
c2=(-y0*D(1,1)+y1)/(D(2,2)-D(1,1));
for t=0:1:10
Timp(t+1)=t+1;
Venit(t+1)=c1*D(1,1)^t+c2*D(2,2)^t+c*(1+r)^t;
Consum(t+1)=s*c1*D(1,1)^(t-1)+c2*D(1,1)^(t-1)+c*(1+r)^(t-1);
end
if ((abs(D(1,1))<1)&(abs(D(2,2))<1))
disp('Traiectorie amortizata');
end
if ((abs(D(1,1))>1)|(abs(D(2,2))>1))
disp('Traiectorie exploziva');
end
end
end
figure(1);
plot(Timp,Venit,'r-*');
title('TRAIECTORIA VENITULUI ');
legend('Venit');
hold on;
figure(2);
plot(Timp,Consum,'r-*');
title('TRAIECTORIA CONSUMULUI ');
legend('Consum');
hold on;
figure(3);
plot3(Timp,Venit,Consum,'r-*');
title('TRAIECTORIA VENIT-CONSUM ');
legend('Venit-Consum');
hold on;
 Bibliografie
Bibliografie
Bazele Ciberneticii Economice - Aplicatii micro si macro economice realizate in mediul Matlab , autori Liliana Spircu si Angela Galupa editura A.S.E., Bucuresti 2002
 2. www.unibuc.ro
2. www.unibuc.ro
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |