Probleme de transport
1. Retele de transport
Definitia 1. Un graf orientat ponderat G = (X, U, c) este o retea de transport daca este conex si exista un singur virf s fara predecesori si un singur virf t fara succesori:
- s I X este intrare in retea si G 1(s) si G (s)
- t I X este iesire din retea astfel incit G 1(t) si G (t)
- pentru orice alt virf x I X (x s si x t), G 1(x) si G (x)
Valoarea c(u) 0 este capacitatea arcului u I U.
Definitia 2. O functie j : U R+ defineste un flux in reteaua G daca:
a) pentru orice arc u I U avem j(u) c(u) (fluxul este compatibil cu reteaua);
b) pentru orice virf x I X (x s si x t) se respecta legea conservarii fluxului:
![]()
unde am notat:
w (x) multimea arcelor incidente interior
virfului x;
w (x) multimea arcelor incidente exterior
virfului x;
Din b) se deduce relatia: ![]()
Valoarea comuna a celor doua sume este valoarea fluxului j si se noteaza v(j
Definitia 3. Un arc u I U pentru care j(u) c(u) se numeste arc saturat.
Problema. In multimea fluxurilor compatibile cu o retea data, exista citeva fluxuri particulare:
- un flux de valoare zero, numit fluxul nul;
- unul sau mai multe fluxuri de valoare maxima, numite fluxuri maxime.
Se cere sa se determine un flux maxim intr-o retea.
Aplicatie. Fie o retea de cale ferata, unde se cunoaste capacitatea fiecarei linii. Care este cantitatea maxima care poate fi transportata de la o statie s la o alta statie t, respectindu-se definitia 2, si cum trebuie organizat transportul?
Exemple
(1) Problema ilustrata in figura 1 are mai multe solutii posibile, fiecare conducind la aceeasi valoare a fluxului maxim: cinci. Capacitatile arcelor exprimate in unitati sint: arcul (x0, x1) - cinci, arcele (x0, x2) si (x2, x3) - doi, si arcele (x1, x2) si (x1, x3) - trei.
In prima solutie se propune transportarea a patru unitati de la x0 la x1, apoi doua unitati se transporta de la x1 la x3, si celelalte doua unitati de la x1 la x2. Din x0 se transporta o unitate la x2, si de aici se preiau trei (doua plus una) unitati care se transporta la x3. Astfel din x0 pleaca cinci unitati care ajung in x3.
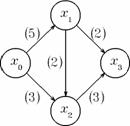
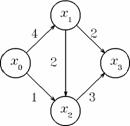
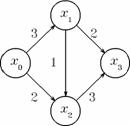
Figura 1. O retea de transport si doua solutii posibile.
(2) Problema ilustrata in figura 2 are o singura solutie. Pe ruta (x0, x1, x4, x5) se transporta o unitate, si pe ruta (x0, x2, x3, x5) se transporta de asemenea o unitate (figura 5).
Aceasta problema va fi folosita ca exemplu in sectiunea 4 pentru implementarea algoritmului Edmonds-Karp.
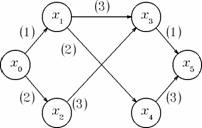
Figura 2. Retea de transport, model pentru algoritmul Edmonds-Karp.
2. Determinarea unui flux maxim
Intr-o problema practica, inainte de a determina fluxul maxim, graful se ajusteaza astfel: se renunta la arcele care intra in virful s, si la arcele care ies din virful t. Inainte de a descrie un algoritm care determina un flux maxim intr-o retea definim notiunea de taietura in retea.
Definitia 4. Fie Y X o submultime cu proprietatea ca s I Y si t Y. Submultimea w (Y ) este o taietura in retea. Capacitatea taieturii este:
c(w (Y )) ![]()
Teorema 1. Pentru orice flux j si orice taietura w (Y) avem:
v j c(w (Y)) (Ford, Fulkerson)
Demonstratie Fiind data o taietura, orice flux trebuie sa o strabata pentru a ajunge de la s la t. Fluxul poate sa satureze unele arce ale retelei, pe altele nu. Daca toate arcele ar fi saturate, am avea v(j c(w (Y)), altfel v(j < c(w (Y)). n
Algoritmul Ford-Fulkerson
Se porneste initial cu fluxul nul. Un flux compatibil oarecare se majoreaza folosind urmatorul procedeu de marcare a virfurilor, virful s fiind intotdeauna marcat:
a) daca x este marcat si (x,y) I U, iar j(x,y) < c(x,y), atunci se marcheaza virful y cu x
b) daca x este marcat si (y,x) I U, iar j(y,x) > 0, atunci se marcheaza virful y cu x
c) daca x este marcat si j(x,y) c(x,y) sau j(y,x) 0, atunci virful y nu se poate marca.
Daca prin acest procedeu se ajunge sa se marcheze virful t, exista un lant m de la s la t cu toate virfurile marcate. Notam cu A submultimea arcelor sale din categoria a) si cu B submultimea arcelor sale din categoria b). Punem:
wa min ;
wb min
w min (wa, wb)
Definim un flux nou j' astfel: j'(u) 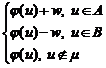
care are proprietatea ca v(j v(j) w
Pentru obtinerea unui flux maxim se repeta aceasta procedura pina cind virful t nu se mai poate marca.
Ramine sa demonstram ca ultimul flux este maxim. Fie acesta y si fie Y submultimea virfurilor care au putut fi marcate in retea dupa introducerea acestui flux. Deoarece s I Y si t Y, se poate defini o taietura w (Y). Avem:
v(y ![]()
Dar ![]() c(u) deoarece altfel s-ar putea continua
marcajul in Y prin arce de categoria
a).
c(u) deoarece altfel s-ar putea continua
marcajul in Y prin arce de categoria
a).
De asemenea ![]() 0 deoarece altfel s-ar putea continua marcajul in Y prin arce de categoria b).
0 deoarece altfel s-ar putea continua marcajul in Y prin arce de categoria b).
Deci v(y) c(w (Y)) si, conform teoremei 1, fluxul y este maxim, iar capacitatea taieturii w (Y ) este minima. Rezulta
Teorema 2 (Ford-Fulkerson, 1956). Intr-o retea de transport, valoarea maxima a fluxului este egala cu capacitatea minima a taieturilor.
In lucrarea Introducere in algoritmi (Cormen et al) sint descrisi in detaliu mai multi algoritmi care determina fluxul maxim. Cei mai eficienti algoritmi folosesc conceptul de preflux. Intr-o prima faza se parcurge reteaua de la s la t si se obtine un pseudoflux, care nu respecta legea conservarii, deoarece are proprietatea:
![]() pentru orice x
s si x t
pentru orice x
s si x t
Cantitatea care intra in virful t coincide cu valoarea fluxului maxim. In faza a doua se parcurge reteaua de la t la s pentru a elimina surplusurile si astfel se obtine un flux maxim.
3. Algoritmul Edmonds-Karp
Algoritmul Ford-Fulkerson nu precizeaza cum se determina lanturile pe care se va mari fluxul - daca se iau in considerare toate lanturile posibile, complexitatea algoritmului poate deveni exponentiala. De aceea au fost elaborate metode de accelerare a acestuia, care conduc la un ordin polinomial de complexitate. O astfel de tehnica a fost elaborata de Edmonds si Karp.
Pentru a determina un lant pe care urmeaza sa se mareasca fluxul se construieste graful ecart al retelei de transport curente. Acest graf are aceeasi multime de virfuri X, si multimea U' a arcelor este definita astfel:
arce de tip (a): daca j(x,y) < c(x,y) atunci (x,y) I U
arce de tip (b): daca j(x,y) > 0 atunci (y,x) I U
Fie un drum
de lungime minima de la s la t in graful ecart, (![]() ,
,![]() , ,
, , ![]() ). Acest drum corespunde unui lant in reteaua
curenta, pe care se poate obtine marirea fluxului. Pe lantul corespondent L(
). Acest drum corespunde unui lant in reteaua
curenta, pe care se poate obtine marirea fluxului. Pe lantul corespondent L(![]() ,
, ![]() , ,
, , ![]() ), care nu este neaparat un drum, se determina:
), care nu este neaparat un drum, se determina:
wa min
wb min
w min (wa, wb
Pe acest lant se mareste fluxul:
j(u) ![]()
Daca nu exista nici un drum intre s si t, algoritmul se incheie si fluxul obtinut este maxim.
Algoritmul de determinare a unui drum de lungime minima reuseste sa marcheze citeva virfuri din graful ecart, cel putin virful s. Cu ajutorul algoritmului Edmonds-Karp se poate determina si taietura de capacitate minima, daca se iau toate arcele cu virfuri initiale din multimea celor marcate si cu virfuri finale din multimea celor nemarcate.
Algoritmul Edmonds-Karp are complexitate teoretica de ordin O(n m2
Tehnici de implementare
Reteaua de transport din figura 2 este folosita ca exemplu pentru a arata cum lucreaza algoritmul Edmonds-Karp. Aceasta retea se reprezinta astfel:
Hr 0 2 4 5 6 7 7
Sr 1 2 3 4 3 5 5
C 1 2 3 2 3 1 3
(0) (1) (2) (3) (4) (5) (6)
Pentru a usura citirea corespondentei dintre reteaua originala si graful ecart am pus in evidenta indicii in masivul Sr.
In figura 3 se marcheaza fluxul nul (stinga) si se construieste graful ecart (dreapta). In graful ecart este marcat un drum de lungime minima - (x0, x1, x3, x5) - cu linie continua, si celelalte arce cu linie intrerupta.
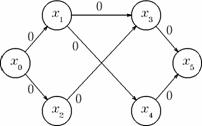
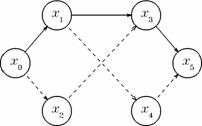
Figura 3. Algoritmul Edmonds-Karp dupa initializare.
Pe acest drum se determina valoarea cu care va fi marit fluxul:
(x0, x1): c(x0,x1) - j(x0,x1) 1 - 0 1
(x1, x3): c(x1,x3) - j(x1,x3) 3 - 0 3
(x3, x5): c(x3,x5) - j(x3,x5) 1 - 0 1
Fluxul va fi marit pe acest drum cu valoarea 1.
Graful ecart din figura 3 se reprezinta astfel:
He 0 2 4 5 6 7 7
Se 1 2 3 4 3 5 5
P 0 1 2 3 4 5 6
(0) (1) (2) (3) (4) (5) (6)
Masivul P are urmatoarea semnificatie. (x,y) este un arc in graful ecart, si succesorul y se afla pe pozitia j in masivul Se: Se[j] y. P[j] indica pozitia arcului corespondent din graful original. In aceasta faza P[j] j (j 0, 1, , n-1) deoarece exista o corespondenta unu la unu intre arcele celor doua grafuri, si orientarile arcelor corespondente coincid.
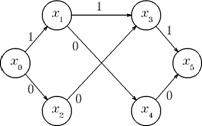
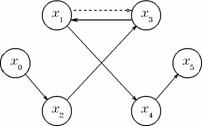
Figura 4. Algoritmul Edmonds-Karp dupa prima iteratie.
In figura 4 se marcheaza fluxul obtinut dupa marire (stinga), si se construieste graful ecart (dreapta). Drumul de lungime minima este (x0, x2, x3, x1, x4, x5). In aceasta figura exista un arc de tip (b) - (x3, x1). Initial fluxul de pe arcul (x0, x1) a fost directionat spre arcul (x1, x3) si apoi spre arcul (x3, x5). La pasul urmator se constata ca de fapt un flux care pleaca pe ruta (x0, x2, x3) nu poate ajunge in x5, si de aceea fluxul care a avut ruta (x0, x1, x3, x5) trebuie redirectionat pe o alta ruta - (x0, x1, x4, x5). Astfel se explica de ce la a doua iteratie drumul determinat in graful ecart este (x0, x2, x3, x1, x4, x5).
Pe acest drum se determina valoarea cu care va fi marit fluxul:
(x0, x2): c(x0,x2) - j(x0,x2) 2 - 0 2
(x2, x3): c(x2,x3) - j(x2,x3) 3 - 0 3
(x3, x1): j(x1,x3) 1 (arcele corespondente au orientari opuse)
(x1, x4): c(x1,x4) - j(x1,x4) 2 - 0 2
(x4, x5): c(x4,x5) - j(x4,x5) 3 - 0 3
Fluxul va fi marit pe acest drum cu valoarea 1.
Graful ecart din figura 4 se reprezinta astfel:
He 0 1 3 4 5 6 6
Se 2 3 4 3 1 5
P 1 2 3 4 2 6
(0) (1) (2) (3) (4) (5)
Sa analizam doua corespondente de arce pentru acest caz.
Arcul (x1, x4) din graful ecart, care corespunde arcului (x1, x4) din retea, este memorat astfel. Pe pozitia j 2 este memorat virful final x4: Se[j] 4. P[j] k 3 indica faptul ca arcul corespondent din retea este memorat pe pozitia k: Sr[k] 4. Ambele arce au acelasi virf final, deci au aceeasi orientare.
Arcul (x3, x1) din graful ecart, care corespunde arcului (x1, x3) din retea, este memorat astfel. Pe pozitia j 4 este memorat virful final x1: Se[j] 1. P[j] k 2 indica faptul ca arcul corespondent din retea este memorat pe pozitia k: Sr[k] 3. Cele doua arce nu au acelasi virf final, deci au orientari opuse.
In figura 5 se observa ca dupa ce s-a marcat fluxul obtinut dupa marire (stinga), si s-a construit graful ecart (dreapta), nu mai exista drumuri de la x0 la x5. In concluzie algoritmul se incheie in aceasta faza, obtinindu-se fluxul maxim de valoare doi.
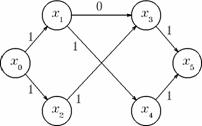
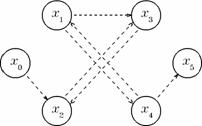
Figura 5. Algoritmul Edmonds-Karp dupa a doua iteratie.
Algoritmul de determinare a unui drum de la x0 la x5 reuseste sa marcheze doar virfurile x0, x2 si x3. Se obtine astfel o taietura formata din arcele (x0, x1) si (x3, x5), care are capacitate doi.
Sinteza. Pentru fiecare arc din graful ecart se memoreaza adresa unde este localizat arcul corespondent din graful original, pentru a putea vedea la examinarea drumului daca doua arce corespondente sint identice sau au orientari opuse.
Arcul (x, y) este memorat pe pozitia k in retea: Sr[k] y. Cele doua situatii posibile se trateaza astfel:
- daca j(x,y) < c(x,y), si y este memorat ca succesor al lui x pe pozitia j, atunci Se[j] y si P[j] k;
- daca j(x,y) > 0, si y este memorat ca succesor al lui x pe pozitia j, atunci Se[j] x si P[j] k.
Pentru a imbunatati performantele algoritmului, graful ecart se reprezinta astfel incit sa fie posibila stergerea unui arc u', care are ca si corespondent in graful original arcul u, in urmatoarele situatii:
- daca u si u' au aceeasi orientare si j(u) c(u) dupa actualizare;
- daca u si u' au orientari opuse si j(u) > 0 dupa actualizare.
Cind nu se mai poate determina un drum intre s si t in graful ecart, acesta se reconstruieste dupa regulile precizate mai sus. Algoritmul se incheie daca dupa reconstruire se obtine un graf ecart in care nu exista nici un drum de la s la t.
Pentru a obtine un graf ecart cu strictul necesar de arce, acesta nu va avea arce care intra in s si nici arce care ies din t.
4. Flux minim intr-o retea de transport
Problema. Fie G (X, U, c) o retea de transport pentru care definim o alta lege a compatibilitatii fluxului: j(u) c(u)
Se cere sa se determine unui flux minim compatibil cu capacitatile arcelor din retea.
Deoarece fluxul nul nu este compatibil, dar respecta legea conservarii fluxului, este nevoie ca intr-o prima faza sa se obtina un flux compatibil.
Se determina un drum m de la s la t care contine cel putin un arc u astfel incit j(u) < c(u). Pe acest drum fluxul se corecteaza astfel:
j'(u) j'(u) w,unde w max
Aceasta procedura se repeta pina cind j(u) c(u) pentru orice arc u I U
Identificarea unor drumuri care sa acopere in final toate arcele retelei este o procedura complexa, deoarece daca reteaua are circuite este nevoie sa se ia in considerare toate arcele aflate pe aceste circuite.
In faza a doua fluxul compatibil se micsoreaza dupa un algoritm asemanator celui care determina un flux maxim. Multimea U' a arcelor grafului ecart se defineste astfel:
a) daca (x,y) I U si j(x,y) > c(x,y), atunci (x,y) I U
b) daca (x,y) I U atunci (y,x) I U
Pe orice arc din categoria (a) fluxul ar putea scadea. Pe de alta parte, pe orice arc fluxul ar putea creste, cu conditia sa existe arce vecine pe care fluxul sa scada in compensatie.
Fie un drum
de la s la t in graful ecart, (![]() ,
,![]() , ,
, , ![]() ). Acest drum corespunde unui lant in reteaua
curenta, pe care se poate obtine micsorarea fluxului. Pe lantul corespondent L(
). Acest drum corespunde unui lant in reteaua
curenta, pe care se poate obtine micsorarea fluxului. Pe lantul corespondent L(![]() ,
, ![]() , ,
, , ![]() ), care nu este neaparat un drum, se determina:
), care nu este neaparat un drum, se determina:
w min
Pe acest lant se micsoreaza fluxul:
j(u) ![]()
Pentru problema fluxului minim nu se cunosc algoritmi de complexitate polinomiala, aceasta fiind NP-completa.
5. Problema de transport pentru graf bipartit
min ![]() cij
0
cij
0
![]() ai 1
i m
ai 1
i m
![]() = bj 1
j n
= bj 1
j n
xij 0 1 i m, 1 j n
unde ![]() =
= ![]() ai
0, bj
0
ai
0, bj
0
Acestei probleme i se asociaza un graf bipartit G (S, D, U, c) unde |S| m, |D| n, si c este o functie cost.
Grafului bipartit i se asociaza un tabel de transport care are m linii si n coloane. Fiecare celula (i, j) contine costul cij si valoarea variabilei xij. Tabelul mai contine o coloana suplimentara in care sint inscrise valorile ai (1 i m), si o linie suplimentara in care sint inscrise valorile bj (1 j n).
Determinarea unei solutii initiale de baza. O solutie a sistemului de m+n ecuatii cu mn necunoscute este o solutie de baza daca masivele coloana ale matricei sistemului corespunzatori componentelor nenule ale solutiei sint liniar independente. Deci o solutie de baza are cel mult m+n-1 componente nenule (acesta este rangul matricei sistemului).
Metoda generala de
obtinere a unei solutii initiale de baza este
urmatoarea. Se fixeaza o celula (i,j) si se atribuie
variabilei xij valoarea ![]() ij min(ai,bj).
Daca
ij min(ai,bj).
Daca ![]() ij ai se
suprima linia i din tabelul de transport si se inlocuieste bj
cu bj ai. Daca
ij ai se
suprima linia i din tabelul de transport si se inlocuieste bj
cu bj ai. Daca ![]() ij bj se
suprima coloana j din tabelul de transport si se inlocuieste ai
cu ai bj. Daca
ij bj se
suprima coloana j din tabelul de transport si se inlocuieste ai
cu ai bj. Daca ![]() ij ai bj
se suprima la alegere linia i sau coloana j. Daca, de exemplu, se
suprima linia i, atunci bj se inlocuieste cu 0.
ij ai bj
se suprima la alegere linia i sau coloana j. Daca, de exemplu, se
suprima linia i, atunci bj se inlocuieste cu 0.
Procedeul se continua pe toate tabelele reduse care se pot obtine in acest mod. Numarul variabilelor care primesc componente nenule prin aceasta metoda este cel mult m n 1.
Metode particulare de obtinere a unei solutii initiale de baza:
a) Metoda coltului de nord-vest. Se alege pentru introducerea in baza a variabilei corespunzatoare celulei situate in prima linie si prima coloana (coltul de nord-vest) a tabelelor reduse.
b) Metoda costului minim. La fiecare pas al metodei generale se selecteaza celula (i,j) corespunzatoare costului minim cij din tabelele reduse.
Notam cu B multimea celulelor (i,j) corespunzatoare variabilelor initializate, si cu S multimea celorlalte celule din tabelul de transport. Graful partial care contine muchiile corespunzatoare celulelor din B este un arbore.
Teorema. Pentru fiecare celula (i,j)IS exista un ciclu elementar unic format de celula (i,j) cu o parte din celulele multimii B. Acest ciclu are proprietatea urmatoare: orice doua celule consecutive se afla pe aceeasi linie sau coloana a tabelului de transport, fara ca trei celule sa se afle pe aceeasi linie sau coloana.
Demonstratie. Teorema este evidenta deoarece:
- daca se adauga o muchie intr-un arbore, se formeaza un ciclu elementar unic;
- un ciclu elementar nu trece de doua ori prin acelasi virf. n
Determinarea unei solutii optime de baza. In aceasta faza fiecare pas al algoritmului de transport efectueaza urmatoarele operatii:
a) Pentru fiecare celula (i,j)IS se determina ciclul m corespunzator. Se marcheaza celulele din ciclu alternativ cu si , incepind cu celula (i,j) care se marcheaza cu . Se determina suma algebrica a costurilor din celulele marcate, avind ca semn marcajul celulelor.
b) Se retine celula (k,l)IS pentru care suma algebrica calculata este minima. Daca suma este pozitiva sau zero, algoritmul se opreste: solutia obtinuta este optima. In caz contrar se determina valoarea w = min .
Fie (p,q) celula pentru care w xpq.
c) Pentru (i,j) celula din ? marcata cu se calculeaza xij xij w.
Pentru (i,j) celula din ? marcata cu se calculeaza xij xij w.
In acest moment variabila xkl intra in baza si variabila xpq iese din baza. Se trece la punctul a).
Daca la sfirsitul pasului b suma algebrica calculata este strict pozitiva, problema de transport are solutie optima unica.
Determinarea tuturor solutiilor optime. Se retine tabelul de transport din momentul obtinerii unei solutii optime. Daca in acest tabel suma algebrica calculata pentru celula (k,l) este 0, se poate obtine o alta solutie optima prin introducerea in baza a variabilei xkl, variabila care iese din baza fiind determinata cu criteriul obisnuit.
Pentru determinarea tuturor solutiilor optime de baza, se cauta in tabelul retinut mai sus toate celulele (k,l)IS pentru care suma algebrica calculata este zero.
Orice solutie optima a problemei de transport este o combinatie liniara convexa a solutiilor optime de baza. Un vector x este combinatie liniara convexa a vectorilor x1, x2, xk daca exista numerele reale l1, l2, lk astfel incit:
0 li 1 pentru 1 i k si ![]() =1, x =
=1, x =![]()
|
Politica de confidentialitate |
| |
Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |