
Modelul lui Kaldor cu preturi anticipate
Un caz particular al modelului lui Kaldor, model care explica mecanismul prin care o piata este reglata prin intermediul preturilor, este acela in care se considera ca oferta nu se orienteaza dupa pretul din perioada anterioara pt-1, ci in raport cu un pret normal pN, pe care producatorul considera ca-l va obtine pe piata.
Modelul Kaldor se scrie in aceasta situatie astfel :
Dt = a+bpt
St = a1 + b1![]()
Dt = St
,unde ![]() reprezinta
pretul "asteptat" de producator si este dat de
relatia:
reprezinta
pretul "asteptat" de producator si este dat de
relatia:
![]() = pt-1 +
c(pN - pt-1) , 0<c<1
= pt-1 +
c(pN - pt-1) , 0<c<1
Cerinte :
Sa se determine ecuatia de dinamica a pretului
Sa se verifice conditiile de existenta ale pretului de echilibru
Analiza stabilitatii pretului in jurul pretului de echilibru
Comparati rezultatele obtinute la punctul 3) cu conditia de stabilitate de la modelul lui Kaldor.
T
Vom avea deci relatiile:
Dt = a+bpt
St = a1 + b1[pt-1 + c(pN - pt-1)]
Dt = St
Inlocuind primele doua relatii ale modelului in cea de-a treia se va obtine succesiv:
a+bpt = a1 + b1pt-1 + b1cpN - b1cpt-1,
bpt - (b1 - b1c)pt-1 = a1 - a + b1cpN
bpt - b1(1 - c)pt-1 = a1 - a + b1cpN
Ultima relatie reprezinta relatia fundamentala de dinamica a modelului kaldorian cu preturi asteptate.
Solutia generala a
ecuatiei neomogene bpt - b1(1 - c)pt-1 =
a1 - a + b1cpN se obtine ca suma a
solutiei generale a ecuatiei omogene bpt - b1(1
- c)pt-1 = 0 si a unei solutii particulare a ecuatiei
neomogene (termenul de neomogenitate este o
pt = ptG + ptP
1. determinarea solutiei generale ptG.
In ecuatia omogena bpt - b1(1 - c)pt-1 = 0 se inlocuieste pt cu λt si se obtine:
bλt - b1(1 - c)λt-1 = 0 T
Tbλ - b1(1 - c) = 0 T
T λ = [b1(1 - c)]/b
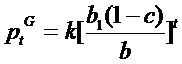
Deoarece ptG = kλt , vom avea:
2. determinarea solutiei particulare ptP.
Se observa ca termenul de
omogenitate este o
ptP =B T bB - b1(1 - c)B = a1 - a + b1cpN T
T B[b - b1(1 - c)] = a1 - a + b1cpN T
T B = (a1 - a + b1cpN)/ [b - b1(1 - c)]
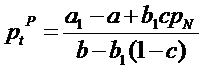
Deci, vom
avea:
3. determinarea solutiei pt a ecuatiei de dinamica a modelului.
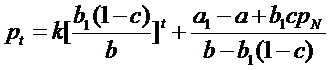
pt
= ptG + ptP T
4. explicitarea solutiei pt a ecuatiei modelului.
La momentul de timp t0 = 0, starea la momentul t0 o vom nota cu p0 si va fi:
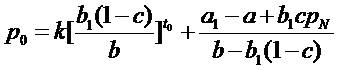
De unde,
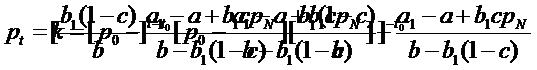
Solutia
finala va fi:
Inlocuind in formula solutiei finale notatia
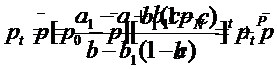
Vom
obtine solutia finala a modelului:
Acest pret p este pretul de echilibru stationar si poate fi interpretat ca un nivel constant al pretului catre care tinde sau nu traiectoria de dinamica a pretuli curent pt.
Analiza dinamicii pietii consta in:
a) studierea existentei pretului de echilibru p;
Conditii de existenta: - b1(1-c)<>b;
p > 0.
b) studierea dinamicii pretului in jurul pretului de echilibru p;
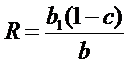
Vom
utiliza notatia:
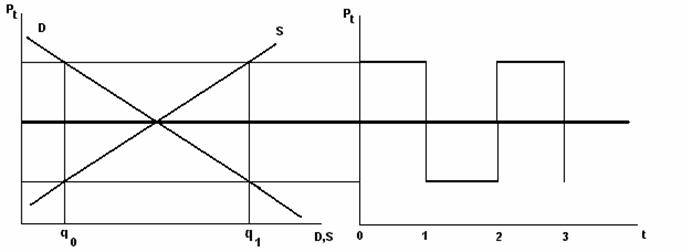
Situatii: i) │R│<1 T comportament convergent monoton daca RI(0,1) si oscilant daca RI(-1,0); in acest caz oscilatiile au o amplitudine din ce in ce mai mica (amortizata):
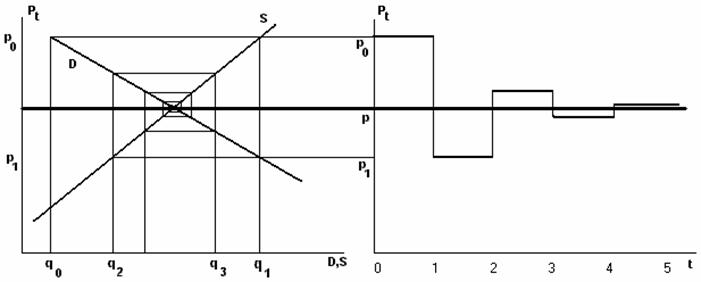
ii) │R│>1 T comportament divergent monoton daca RI(0,1) si oscilant daca RI(-1,0); in acest caz oscilatiile au o amplitudine din ce in ce mai mare (exploziva):
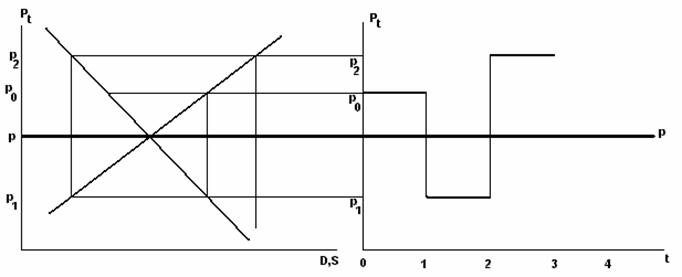
iii) │R│=-1 T oscilatiile au amplitudine
iiii) R = 1 T nu exista pret de echilibru (p=p0).
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |