
Proprietati ale functiilor elementare
1. Functii polinomiale
Definitie:
Functia f: R →
R, f(x)= anxn+ an-1xn-1+ an-2xn-2+..+
a1x1+ a0x0 se numeste functie polinomiala
de gradul n de coeficienti ai ![]() R, n
R, n ![]() N, an
N, an![]() 0 si variabila x.
0 si variabila x.
In functie de gradul polinomul asociat, functia are proprietati de monotonie, convexitate si concavitate, bijectivitate si continuitate diferite, de aceea in prezenta lucrare, la aceasta sectiune voi prezenta cazul functiiilor de gradul I , II si functia putere cu exponent natural ca si cazuri particulare a functiei polinomiale.
1.1 Functia liniara sau functia de gradul I.
Definitie:
Functia f: R →
R, f(x)= ax+b se numeste
functie de gradul I de coeficienti a,b ![]() R. In tabelul de mai jos regasim principalele
caracteristici:
R. In tabelul de mai jos regasim principalele
caracteristici:
|
Functia |
f: R → R, f(x) = ax+b unde a,b |
||
|
Intersectia cu axele De coordonate Ox si Oy |
Gf Gf |
||
|
Convexitate si concavitate |
Si convexa si concava in acelasi timp. |
||
|
Paritate |
Cand b = 0 functia este impara, Gf fiind simetric fata de O(0,0), in rest nu se pune problema. |
||
|
Monotonia functiei |
a< 0 |
x |
- |
|
f(x)=ax+b |
+ |
||
|
a >0 |
x |
- |
|
|
f(x)=ax+b |
- |
||
|
Semnul functiei |
x |
- |
|
|
f(x)=ax+b |
Semn opus a 0 acelasi semn a |
||
|
Continuitate |
Gf este o dreapta continua |
||
|
Bijectivitate |
Da |
||
Observatie: In cazul a=0 functia este constanta, Gf fiind o dreapta ││Ox.
1.2. Functia de gradul II.
Definitie: Functia f: R → R, f(x)= ax2+bx+c se numeste functie de gradul II de
coeficienti a,b,c ![]() R. cu a≠ 0.
R. cu a≠ 0.
|
Functia |
f: R → R, f(x)= ax2+bx+c, a,b,c |
||||||
|
Calculul discriminantului ∆ |
∆=b2-4ac |
||||||
|
∆ >0 |
∆=0 |
∆<0 |
|||||
|
Varful parabolei |
V( Daca a > 0 V - punct de minim Daca a < 0 V - punct de maxim |
V( Daca a > 0 V - punct de minim Daca a < 0 V - punct de maxim |
V( Daca a > 0 V - punct de minim Daca a < 0 V - punct de maxim |
||||
|
Intersectia cu axele de coordonate |
Gf
A1(x1,0)
si A2(x2,0) Gf
|
Gf A1=A2= V( Gf
|
Gf Gf nu intersecteaza axa Ox Gf
|
||||
|
Monotonia functiei de gradul II |
x = |
x = |
x = |
||||
|
a > 0 |
x |
- |
|||||
|
f(x) |
+ |
||||||
|
a < 0 |
x |
- |
|||||
|
f(x) |
+ |
||||||
|
Semnul functiei |
x |
- |
x |
- |
x |
- |
|
|
f(x) |
sgn(a) 0 -sgn(a) 0 sgn(a) |
f(x) |
sgn(a) 0 sgn(a) |
f(x) |
sgn(a) sgn(a) sgn(a) |
||
|
Bijectivitate |
NU |
||||||
|
Continuitate |
Gf este o curba continua numita parabola |
||||||
1.3 Functia putere cu exponent numar natural.
Definitie:
Functia f: R →
R, f(x)=xn cu n![]() N* se numeste functie putere cu exponent
numar natural.
N* se numeste functie putere cu exponent
numar natural.
In tabelul de mai jos voi reda principalele atribute ce caracterizeaza aceasta functie:
|
Functia |
f: R → R, f(x)=x2k, n |
f: R → R, f(x)=x2k+1, n |
||
|
Intersectia cu axele de coordonate Ox si Oy |
O(0,0) |
O(0,0) |
||
|
Paritate |
f(-x)=f(x) functie para |
f(-x)=-f(x) functie impara |
||
|
Simetria graficului Gf |
Gf simetric fata de Oy |
Gf simetric fata de O |
||
|
Convexitate si concavitate |
Convexa pe R |
Concava pe (- Convexa pe [0,+ O(0,0) punct de inflexiune |
||
|
Puncte remarcabile pe graficul functiei |
(-1,1), (0,0), (1,1) |
(-1,-1), (0,0), (1,1) |
||
|
Ordonarea puterilor pe (0,1)
si (1, |
Pentru 0< x < 1 Pentru x > 1 |
Pentru 0< x < 1 Pentru x > 1 |
||
|
Monotonia functiei |
x |
- |
x |
- |
|
x2k |
+ |
x2k+1 |
+ |
|
|
Strict descr. pe (- Strict cresc. pe [0,+ (0,0) punct de minim |
Strict crescatoare pe R (0,0) punct de inflexiune |
|||
|
Semnul functiei |
x |
- |
x |
- |
|
x2k |
+ |
x2k+1 |
+ |
|
|
Continuitate |
Gf este o curba continua |
Gf este o curba continua |
||
2. Functia putere cu exponent numar intreg negativ.
Definitie:
Functia f: R →
R, f(x)=x-n cu n![]() N* se numeste functie putere cu exponent
numar intreg negativ.
N* se numeste functie putere cu exponent
numar intreg negativ.
|
Functia |
f: R* → R*, f(x)= n |
f: R* → R*, f(x)= n |
||
|
Intersectia cu axele de coordonate Ox si Oy |
Nu taie axele de coordonate |
Nu taie axele de coordonate |
||
|
Paritate |
f(-x)=f(x) functie para |
f(-x)=-f(x) functie impara |
||
|
Simetria graficului Gf |
Gf simetric fata de Oy |
Gf simetric fata de O |
||
|
Convexitate si concavitate |
Convexa pe R* |
Concava pe (- Convexa pe [0,+ O(0,0) punct de inflexiune |
||
|
Puncte remarcabile pe graficul functiei |
(-1,1), (1,1) |
(-1,-1), (1,1) |
||
|
Comportament asimptotic |
x=0 asimptota verticala y=0 asimptota orizontala |
x=0 asimptota verticala y=0 asimptota orizontala |
||
|
Ordonarea puterilor pe (0,1)
si (1, |
Pentru 0< x < 1 Pentru x > 1 |
|||
|
Monotonia functiei |
x |
- |
x |
- |
|
|
0 ↑
1 ↑+ |
|
0 ↓
-1 ↓- |
|
|
Strict cresc. pe (- Strict descresc. pe [0,+ |
Strict descrescatoare pe R* |
|||
|
Semnul functiei |
x |
- |
x |
- |
|
|
+ |
|
+ |
|
|
Continuitate |
Gf este o curba continua pe (- |
Gf este o curba continua pe (- |
||
|
Bijectivitate |
Nu |
Da |
||
3. Functia radical de ordinul n.
Definitie:
a) Functia f: R → R, f(x)=![]() , n
, n![]() N*, se numeste functia radical de ordin impar.
N*, se numeste functia radical de ordin impar.
b) Functia f: [0,+![]() ) → [0,+
) → [0,+![]() ), f(x)=
), f(x)=![]() n
n![]() N*, se numeste functia radical de ordin par.
N*, se numeste functia radical de ordin par.
|
Functia |
f: [0,+ f(x)= |
f: R → R, f(x)= |
||
|
Intersectia cu axele de coordonate Ox si Oy |
O(0,0) |
O(0,0) |
||
|
Paritate |
Nu |
f(-x)=-f(x) functie impara |
||
|
Simetria graficului Gf |
Nu |
Gf simetric fata de O |
||
|
Convexitate si concavitate |
Concava pe [0,+ |
Convexa pe (- Concava pe [0,+ |
||
|
Puncte remarcabile pe graficul functiei |
(0,0), (1,1) |
(-1,-1), (0,0), (1,1) |
||
|
Monotonia functiei |
x |
- |
x |
- |
|
|
0
↑ ↑ 1 ↑ ↑ + |
|
- |
|
|
Strict cresc. pe [0,+ |
Strict crescatoare pe R |
|||
|
Semnul functiei |
x |
0 + |
x |
- |
|
|
0+ + + + + + + + + |
|
- |
|
|
Continuitate |
Gf este o curba continua |
Gf este o curba continua |
||
|
Bijectivitate |
Da |
Da |
||
|
Functia inversa |
f-1: [0,+ f-1(x) = x2n |
f: R → R, f-1(x) = x2n+1 |
||
4. Functia putere cu exponent rational.
Definitie:
f: (0,+![]() ) → R, f(x)=
) → R, f(x)= ![]() unde m
unde m![]() Z, n
Z, n ![]() N* cu n≥2, se
numeste functia putere cu exponent rational.
N* cu n≥2, se
numeste functia putere cu exponent rational.
Observatii:
1.
Daca m,n ≥2
atunci are sens ![]()
![]() x > 0, in acest caz proprietati
asemanatoare cu a functiei cu exponent natural.
x > 0, in acest caz proprietati
asemanatoare cu a functiei cu exponent natural.
2. Daca m = 1 atunci se obtine functia radical de ordinul n.
3. Daca m < 0 in acest caz functia manifesta proprietati asemanatoare cu a functiei cu exponent intreg negativ.
In graficul de mai jos am efectuat un studiu comparativ al comportarii functiilor:
x2 (albastru), x3/2(rosu), x3(verde), x-3/2(negru) .
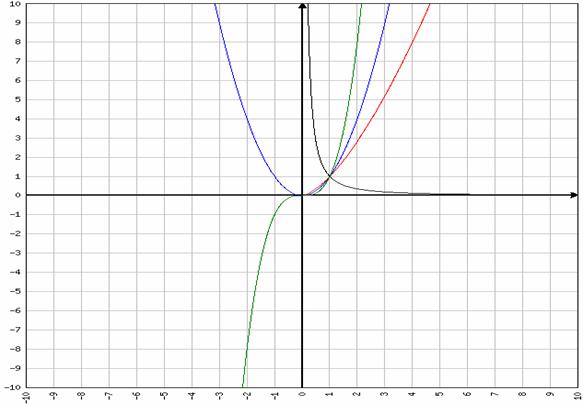
Concluzii:
1. Pentru x > 1 si m,n ![]() N* rezulta
N* rezulta ![]() > 1
> 1
2. Pentru 0 < x < 1 si m,n ![]() N* rezulta
N* rezulta ![]() < 1
< 1
3. Pentru x > 1 si r1 < r2 cu r1 ,r2 ![]() Q atunci x r1 < x r2
Q atunci x r1 < x r2
4.
Pentru 0 < x < 1 si r1 < r2 cu r1 ,r2 ![]() Q atunci x r1 > x r2
Q atunci x r1 > x r2
Functia exponentiala.
Definitie:
Fie a > ![]() ),f(x) = ax, se numeste functie
exponentiala de baza a.
),f(x) = ax, se numeste functie
exponentiala de baza a.
Studiul functiei se face pentru doua cazuri, in functie de baza a.
|
Functia |
f:
R → (0,+ 0 < a < 1 |
f:
R → (0,+ a > 1 |
|
Intersectia cu axele de coordonate |
Gf Gf |
Gf Gf |
|
Semnul functiei |
ax > 0 |
ax > 0 |
|
Convexitate si concavitate |
Convexa |
Convexa |
|
Monotonie |
Strict descrescatoare |
Strict crescatoare |
|
Comportament asimptotic |
y = 0 asimptota orizontala la |
y = 0 asimptota orizontala la |
|
Continuitate |
Gf este o curba continua |
Gf este o curba continua |
|
Bijectivitate |
Da |
Da |
|
Functia inversa |
f-1: (0,
+ f-1 (x)= loga x |
f-1: (0,
+ f-1 (x)= loga x |
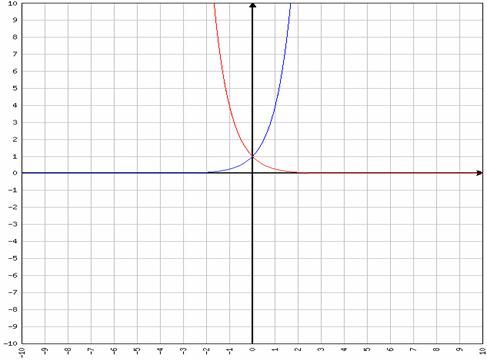
Exemplu:
f1: R →
(0,+![]() ), f(x) = 4x (grafic culoare albastra)
si f2: R → (0,+
), f(x) = 4x (grafic culoare albastra)
si f2: R → (0,+![]() ),f(x) = 4-x
(grafic culoare rosie)
),f(x) = 4-x
(grafic culoare rosie)
6. Functia logaritmica.
Definitie: Fie a > 0, a≠1.
Functia f: (0, +![]() ) → R
definita prin f(x)= loga x, se numeste functie
logaritmica in baza a.
) → R
definita prin f(x)= loga x, se numeste functie
logaritmica in baza a.
|
Functia |
f: (0,
+ f(x)= loga x |
f: (0,
+ f(x)= loga x |
||
|
Intersectia cu axele de coordonate |
Gf
Gf nu taie axa Oy |
Gf
Gf nu taie axa Oy |
||
|
Convexitate si concavitate |
Convexa |
Concava |
||
|
Monotonie |
Strict descrescatoare |
Strict crescatoare |
||
|
Semnul functiei logaritmice |
x |
0 1 |
x |
0 1 |
|
loga x |
|
loga x |
|
|
|
Bijectivitate |
Da |
Da |
||
|
Functia inversa |
f-1: R → (0, + f-1(x) = ax cu 0 < a < 1 |
f-1: R → (0, + f-1(x) = ax cu a > 1 |
||
|
Comportament asimptotic |
Axa Oy este asimptota verticala
la |
Axa Oy este asimptota verticala
la |
||
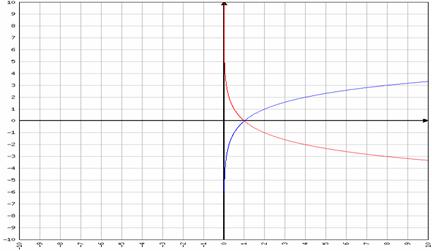 Exemplu:
f1: R →
(0,+
Exemplu:
f1: R →
(0,+![]() ), f1(x) = log4x (grafic culoare
albastra) si f2: R → (0,+
), f1(x) = log4x (grafic culoare
albastra) si f2: R → (0,+![]() ),f2(x) = log1/4x (grafic culoare rosie)
),f2(x) = log1/4x (grafic culoare rosie)
7. Functii trigonometrice directe.
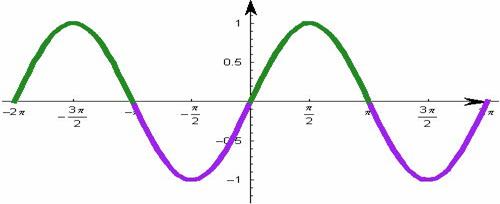
7.1. Functia sinus.
Definitie: Functia f: R → [-1;1] desrisa de forma analitica f(x)=sinx se numeste functia sinus.
|
Proprietati |
pe [0.2Π) |
pe R |
|
|
Intersectia graficului cu axele de coordonate |
Gf
Gf |
Gf Bk(kΠ,0) Gf |
|
|
Paritate |
Nu se pune problema |
Impara |
|
|
Simetria graficului |
Nu se pune problema |
Gf simetric in raport cu O(0,0) |
|
|
Monotonia functiei ↑- f.strict cresc. ↓- f.strict descresc. |
x |
0 Π/2 Π 3Π/2 2Π |
|
|
f(x) |
0 ↑ 1 ↓ 0 ↓-1 ↑ 0 |
||
|
|
|||
|
Marginire. Valori extreme |
Functie marginita -1≤ f(x) ≤ 1 Max f(x) =1 = f(Π/2) Min f(x) =-1 = f(3Π/2) |
Functie marginita -1≤ f(x) ≤ 1 Max f(x)=1=f(Π/2+2kΠ Min f(x)=-1= f(3Π/2+2kΠ |
|
|
Convexitate si Concavitate |
-concava pe [0,Π] -convexa pe Π,2Π] x Π punct de inflexiune |
-concava pe -convexa pe x Π+2kΠ puncte de inflexiune |
|
|
Continuitate |
continua |
Continua |
|
|
Rezolvarea ecuatiei |
x1=0 si x2=Π |
x 1,k=2kΠ si x 2,k=Π+2kΠ |
|
|
Semnul functiei |
sinx >0 pentru x є (0,Π sinx <0 pentru x є (Π,2Π |
sinx >0 pentru x є (2kΠ Π+2kΠ sinx <0 pentru x є (Π+2kΠ,2Π+2kΠ |
|
|
Bijectivitate |
Nu |
Nu |
|
|
Restrictii bijective |
|
|
|
Observatii:
Daca x1,x2єR,
atunci are loc inegalitatea lui Jensen: ![]()
7.2. Functia cosinus.
Definitie: Functia f: R → [-1;1] desrisa de forma analitica f(x)=cosx se numeste functia cosinus.
|
Proprietati |
pe [0.2Π) |
pe R |
|
|
Intersectia graficului cu axele de coordonate |
Gf
Gf |
Gf Dk(3Π/2+2kΠ,0) Gf |
|
|
Paritate |
Nu se pune problema |
para |
|
|
Simetria graficului |
Nu se pune problema |
Gf simetric in raport cu axa Oy |
|
|
Monotonia functiei ↑- f.strict cresc. ↓- f.strict descresc. |
x |
0 Π/2 Π 3Π/2 2Π |
|
|
f(x) |
1 ↓ 0 ↓ -1 ↑ 0 ↑ 1 |
||
|
|
|||
|
Marginire. Valori extreme |
Functie marginita -1≤ f(x) ≤ 1 Max f(x) =1 = f(0 Min f(x) =-1 = f(Π |
Functie marginita -1≤ f(x) ≤ 1 Max f(x)=1=f(2kΠ Min f(x)=-1= f(Π+2kΠ |
|
|
Convexitate si Concavitate |
-concava pe [0,Π/2] si [3Π/2,2Π -convexa pe [Π/2,3Π/2 x Π/2 si x=3Π/2 puncte de inflexiune |
-concava pe -convexa pe
|
|
|
Continuitate |
Continua |
Continua |
|
|
Rezolvarea ecuatiei |
x1=Π/2 si x2=3Π/2 |
x 1,k=Π /2+2kΠ si x 2,k=3Π /2+2kΠ |
|
|
Semnul functiei |
cosx >0 pentru x є (0,Π/2) si pe (3Π/2,2Π cosx <0 pentru x є (Π/2,3Π/2 |
cosx >0 pentru x є cosx <0 pentru x є |
|
|
Bijectivitate |
Nu |
Nu |
|
|
Restrictii bijective |
|
|
|
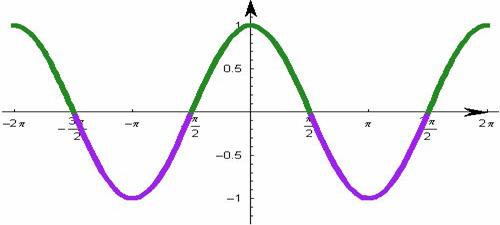
Observatii:
Daca x1,x2є(-Π/2,Π/2)
atunci are loc inegalitatea lui Jensen: ![]()
7.3. Functia tangenta.
Functia f:R- ![]()
![]() R, descrisa de
f(x)=
R, descrisa de
f(x)=![]() se numeste functia tangenta. Aceasta este o
functie periodica de perioada principala T0=Π.Prin urmare studiul acestei functii se va
realiza pe un interval de lungime Π. Prezint in cele ce urmeaza principalele
proprietati in tabelul de mai jos.
se numeste functia tangenta. Aceasta este o
functie periodica de perioada principala T0=Π.Prin urmare studiul acestei functii se va
realiza pe un interval de lungime Π. Prezint in cele ce urmeaza principalele
proprietati in tabelul de mai jos.
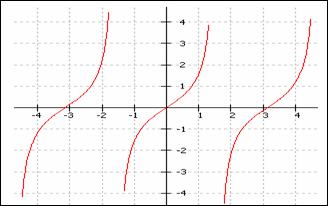
Graficul functiei f(x) = tg x
|
Proprietati |
pe (-Π/2.Π/2) |
pe D |
|
|
Intersectia graficului cu axele de coordonate |
Gf Gf |
Gf Bk(kΠ,0) Gf |
|
|
Paritate |
Impara |
Impara |
|
|
Simetria graficului |
Gf simetric in raport cu O(0,0) |
Gf simetric in raport cu O(0,0) |
|
|
Monotonia functiei ↑- f.strict cresc. ↓- f.strict descresc. |
x |
Π/2 Π/4 0 Π/4 Π/2 |
|
|
f(x) |
- |
||
|
|
|||
|
Marginire. Valori extreme |
Functie nemarginita x= Π/2 si x=Π/2 asimptote verticale |
Functie nemarginita x= |
|
|
Convexitate si Concavitate |
-concava pe (-Π/2,0) -convexa pe [0,Π/2) x=0 punct de inflexiune |
-concava pe -convexa pe x kΠ puncte de inflexiune |
|
|
Continuitate |
continua |
Curba discontinua |
|
|
Rezolvarea ecuatiei |
x1=0 |
x k=kΠ |
|
|
Semnul functiei |
tgx >0 pentru x є (-Π/2,0) tgx <0 pentru x є (0,Π/2) |
tgx >0 pentru x є tgx <0 pentru x є
|
|
|
Bijectivitate |
Da |
Nu |
|
|
Restrictii bijective |
|
|
|
7.4. Functia cotangenta.
Functia f:R- ![]()
![]() R, descrisa de
f(x)=
R, descrisa de
f(x)=![]() se numeste functia cotangenta. Aceasta este o
functie periodica de perioada principala T0=Π. Prin urmare studiul acestei functii se va
realiza pe un interval de lungime Π,
acesta fiind (0, Π ). Prezint in cele ce urmeaza principalele
proprietati ale functiei in tabelul de mai jos.
se numeste functia cotangenta. Aceasta este o
functie periodica de perioada principala T0=Π. Prin urmare studiul acestei functii se va
realiza pe un interval de lungime Π,
acesta fiind (0, Π ). Prezint in cele ce urmeaza principalele
proprietati ale functiei in tabelul de mai jos.
|
Proprietati |
pe (0.Π) |
pe D |
|
|
Intersectia graficului cu axele de coordonate |
Gf A(Π/2,0) Gf |
Gf Bk(Π/2 kΠ,0) Gf |
|
|
Paritate |
Nu |
Impara |
|
|
Simetria graficului |
Nu |
Gf simetric in raport cu O(0,0) |
|
|
Monotonia functiei ↑- f.strict cresc. ↓- f.strict descresc. |
x |
0 Π/2 Π |
|
|
f(x) |
|
||
|
↓- f.strict descresc. |
|||
|
Marginire. Valori extreme |
Functie nemarginita x=0 si x=Π asimptote verticale |
Functie nemarginita x= k Π asimptote verticale |
|
|
Convexitate si Concavitate |
-convexa pe (0,Π/2 -concava pe [Π/2,Π x=Π/2 punct de inflexiune |
-concava pe -convexa pe x Π/2+kΠ puncte de inflexiune |
|
|
Continuitate |
Continua |
Curba discontinua |
|
|
Rezolvarea ecuatiei |
x= Π/2 |
x k= Π/2+kΠ |
|
|
Semnul functiei |
ctgx >0 pentru x є (0,Π/2) ctgx <0 pentru x є (Π/2, Π |
ctgx >0 pentru x є
ctgx <0 pentru x є
|
|
|
Bijectivitate |
Da |
Nu |
|
|
Restrictii bijective |
|
|
|
Observatie:
Intre functiile
tangenta si cotangenta ale aceluiasi argument avem
urmatoarea relatie de legatura : tgx*ctgx=1 pentru x![]() si x
si x![]() cu k
cu k![]()
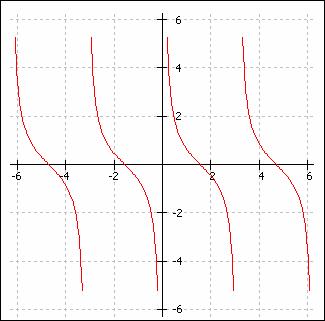
Graficul functiei f(x) = ctg x
8. Functii trigonometrice inverse
8.1.
Functia arcsinus. Functia
sinx:![]() este o functie bijectiva deci
inversabila. Inversa acestei
functii este functia arcsinx:
este o functie bijectiva deci
inversabila. Inversa acestei
functii este functia arcsinx: ![]() definita de
arsiny=x daca si numai daca sinx=y. Graficele functiilor arcsinx si
sinx sunt simetrice fata de prima bisectoare.
definita de
arsiny=x daca si numai daca sinx=y. Graficele functiilor arcsinx si
sinx sunt simetrice fata de prima bisectoare.
Principalele proprietati ale functiei arcsinx sunt redate in tabelul de mai jos.
|
Proprietati |
|
|
Intersectia graficului cu axele de coordonate |
Gf Gf |
|
Paritate |
impara |
|
Simetria graficului |
In raport cu O(0,0) |
|
Monotonia functiei ↑- f.strict cresc. ↓- f.strict descresc. |
- f.strict crescatoare pe |
|
Marginire. Valori extreme |
Functie marginita
Min f(x)= |
|
Convexitate si Concavitate |
-convexa pe 0,1 -concava pe [-1 0 x=0 punct de inflexiune |
|
Continuitate |
Continua |
|
Rezolvarea ecuatiei |
arcsinx= 0 |
|
Semnul functiei |
arcsinx arcsinx |
|
Bijectivitate |
Da |
|
Functia inversa |
sinx: |
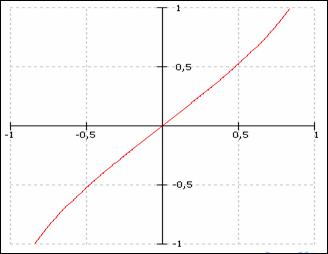
Graficul functiei f(x) = arcsin x
8.2.
Functia arccosinus. Functia
cosx:![]() este o functie bijectiva deci inversabila. Inversa acestei functii este
functia arccosx:
este o functie bijectiva deci inversabila. Inversa acestei functii este
functia arccosx: ![]() definita de
arccosy=x daca si numai daca cosx=y. Graficele functiilor arccosx si
cosx sunt simetrice fata de prima bisectoare. Principalele
proprietati ale functiei arcsinx sunt redate in tabelul de mai
jos.
definita de
arccosy=x daca si numai daca cosx=y. Graficele functiilor arccosx si
cosx sunt simetrice fata de prima bisectoare. Principalele
proprietati ale functiei arcsinx sunt redate in tabelul de mai
jos.
|
Proprietati |
|
|
Intersectia graficului cu axele de coordonate |
Gf Gf |
|
Paritate |
Nu |
|
Simetria graficului |
In raport cu C(0, |
|
Monotonia functiei ↑- f.strict cresc. ↓- f.strict descresc. |
- f.strict descrescatoare pe |
|
Marginire. Valori extreme |
Functie marginita
Min f(x)= 0 Max
f(x)= |
|
Convexitate si Concavitate |
-concava pe 0,1 -convexa pe [-1 0 x=0 punct de inflexiune |
|
Continuitate |
Continua |
|
Rezolvarea ecuatiei |
arccosx= 0 |
|
Semnul functiei |
arccos |
|
Bijectivitate |
Da |
|
Functia inversa |
cosx: |
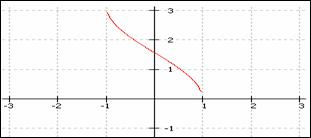
Graficul functiei f(x) = arccos x
8.3.
Functia arctangenta. Functia tgx:![]() este o functie bijectiva deci
inversabila. Inversa acestei
functii este functia arctgx:
este o functie bijectiva deci
inversabila. Inversa acestei
functii este functia arctgx: ![]() definita de arctgy=x daca si numai daca
tgx=y. Graficele functiilor arctgx
si tgx sunt simetrice fata de prima bisectoare. Principalele proprietati ale
functiei arctgx sunt redate in tabelul de mai jos.
definita de arctgy=x daca si numai daca
tgx=y. Graficele functiilor arctgx
si tgx sunt simetrice fata de prima bisectoare. Principalele proprietati ale
functiei arctgx sunt redate in tabelul de mai jos.
|
Proprietati |
R |
|
Intersectia graficului cu axele de coordonate |
Gf Gf |
|
Paritate |
Impara |
|
Simetria graficului |
In raport cu O(0,0) |
|
Monotonia functiei ↑- f.strict cresc. ↓- f.strict descresc. |
- f.strict crescatoare pe R |
|
Marginire. Valori extreme |
Functie marginita
x= x=- |
|
Convexitate si Concavitate |
-convexa pe - -concava pe [0, + x=0 punct de inflexiune |
|
Continuitate |
Continua |
|
Rezolvarea ecuatiei |
arctgx= 0 |
|
Semnul functiei |
arctgx < 0
pentru x arctgx > 0
pentru x |
|
Bijectivitate |
Da |
|
Functia inversa |
tgx: |
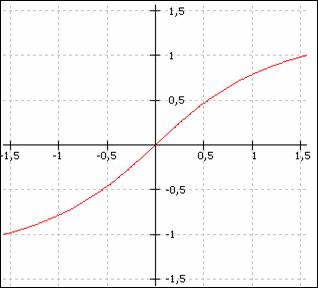
Graficul functiei f(x) = arctg x
8.4.
Functia arccotangenta.Functia ctgx:![]() este o functie bijectiva deci
inversabila. Inversa acestei
functii este functia arcctgx:
este o functie bijectiva deci
inversabila. Inversa acestei
functii este functia arcctgx: ![]() definita de
arcctgy=x daca si numai daca ctgx=y. Graficele functiilor arcctgx si
ctgx sunt simetrice fata de prima bisectoare. Principalele proprietati ale
functiei arctgx sunt redate in tabelul de mai jos.
definita de
arcctgy=x daca si numai daca ctgx=y. Graficele functiilor arcctgx si
ctgx sunt simetrice fata de prima bisectoare. Principalele proprietati ale
functiei arctgx sunt redate in tabelul de mai jos.
|
Proprietati |
R |
|
Intersectia graficului cu axele de coordonate |
Gf Gf |
|
Paritate |
Nu |
|
Simetria graficului |
In raport cu C(0, |
|
Monotonia functiei ↑- f.strict cresc. ↓- f.strict descresc. |
- f.strict descrescatoare pe R |
|
Marginire. Valori extreme |
Functie marginita
y=0 asimptota orizontala la + y= |
|
Convexitate si Concavitate |
-concava pe - -convexa pe [0, + x=0 punct de inflexiune |
|
Continuitate |
Continua |
|
Rezolvarea ecuatiei |
arcctgx= 0 nu are solutie |
|
Semnul functiei |
arcctgx > 0
pentru x |
|
Bijectivitate |
Da |
|
Functia inversa |
ctgx: |
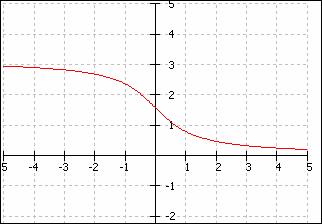
Graficul functiei f(x) = arcctg x
9. Functii speciale. In continuare prezint o serie de functii a caror proprietati sunt utile si prezente in programa de gimnaziu si liceu.
9.1. Functia valoare absoluta
Definitie: Functia f:R![]()
![]() descrisa de
f(x)=max(x,-x)=
descrisa de
f(x)=max(x,-x)=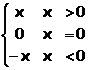 se numeste functie modul sau functie valoare
absoluta. Aceasta se mai noteaza si astfel: f(x)=
se numeste functie modul sau functie valoare
absoluta. Aceasta se mai noteaza si astfel: f(x)=![]()
Proprietati:
Teorema modulului
1. ![]()
![]()
![]() ;
; ![]() = 0
= 0 ![]() x=0;
x=0;
2. Daca x,y ![]() R atunci
R atunci ![]() ;
;
3. Daca x,y ![]() R atunci
R atunci ![]() ;
;
4. Daca x,y ![]() R atunci
R atunci ![]() pentru
pentru ![]()
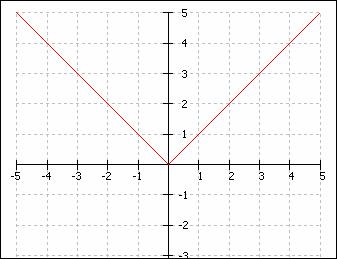
Din punct de vedere grafic functia valoare absoluta se prezinta astfel:
|
Proprietati |
R |
|
Intersectia graficului cu axele de coordonate |
Gf Gf |
|
Paritate |
Para |
|
Simetria graficului |
In raport cu Oy |
|
Monotonia functiei ↑- f.strict cresc. ↓- f.strict descresc. |
f.strict descrescatoare pe (- f.strict crescatoare pe (0, |
|
Marginire. |
Functie
marginita inferior |
|
Convexitate si Concavitate |
-convexa pe R |
|
Continuitate |
Continua |
|
Rezolvarea ecuatiei |
|
|
Semnul functiei |
|
|
Bijectivitate |
Nu |
9.2. Functia caracteristica a unei multimi.
Definitie: Functia f:A![]() descrisa de fA(x)=
descrisa de fA(x)=![]() se numeste functie caracteristica
multimii A.
se numeste functie caracteristica
multimii A.
Teorema: Fie A,B submultimi ale unei multimi E.
Atunci A=B daca si numai daca fA(x)= fB(x);
Observatie: A demonstra ca doua multimi sunt egale e echivalent cu a demonstra ca functiile lor caracteristice sunt egale.
Amintim aici functia lui
Dirichlet f(x)= ![]() este periodica avand ca perioada orice numar
rational.(sau functia caracteristica a multimii Q care este
o functie para, marginita, surjectiva)
este periodica avand ca perioada orice numar
rational.(sau functia caracteristica a multimii Q care este
o functie para, marginita, surjectiva)
9.3. Functia parte intreaga, functia parte fractionara.
Definitie: Functia f: R![]() Z data de legea f(x)=
Z data de legea f(x)=![]() unde
unde ![]() reprezinta cel
mai mare intreg mai mic decat x, se numeste functie parte
intreaga.
reprezinta cel
mai mare intreg mai mic decat x, se numeste functie parte
intreaga.
Definitie: Functia f: R![]()
![]() data de legea
f(x)= x-
data de legea
f(x)= x-![]() unde
unde ![]() reprezinta cel
mai mare intreg mai mic decat x, se numeste functie parte
fractionara.
reprezinta cel
mai mare intreg mai mic decat x, se numeste functie parte
fractionara.
Proprietati ale functiei parte intreaga:
1. ![]() ;
;
2. ![]() ;
;
3. ![]()
4. ![]()
![]()
9.4. Functia signum.
Definitie: Functia f:A![]() descrisa de sgn x=
descrisa de sgn x=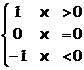 se numeste functie signum (indicator de semn).
se numeste functie signum (indicator de semn).
Proprietati: Functia signum este surjectiva dar neinjectiva, impara si sgn(x*y)=sgn(x)*sgn(y)
|
Politica de confidentialitate |
| |
Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |