Serii cu termeni pozitivi. Exemple
Fie ![]() . Seria geometrica
. Seria geometrica ![]() este convergenta
daca si numai daca
este convergenta
daca si numai daca ![]() . In cazul cand
. In cazul cand ![]() , suma seriei este egala cu
, suma seriei este egala cu ![]() .
.
Solutie. Daca ![]() , atunci termenul general al seriei nu converge la zero
si deci, seria nu este convergenta. Daca
, atunci termenul general al seriei nu converge la zero
si deci, seria nu este convergenta. Daca ![]() , atunci
, atunci ![]() si sirul
sumelor partiale are suma
si sirul
sumelor partiale are suma 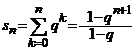 .
.
De
aici deducem ca suma seriei este
egala cu ![]() .
.
Aratati
ca seria 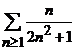 este
divergenta.
este
divergenta.
Intr-adevar,
definim ![]() si
si ![]() . Atunci, avem
. Atunci, avem ![]() . Din criteriul
I de comparatie nu putem trage concluzii asupra
convergentei seriei. Cu ajutorul criteriului
III, obtinem
. Din criteriul
I de comparatie nu putem trage concluzii asupra
convergentei seriei. Cu ajutorul criteriului
III, obtinem ![]() , deci seriile
, deci seriile ![]() si
si ![]() au aceeasi
natura, ultima serie fiind divergenta ( !).
au aceeasi
natura, ultima serie fiind divergenta ( !).
Seria 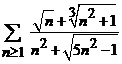 este
convergenta.
este
convergenta.
Se compara
aceasta serie cu seria convergenta ![]() si,
dupa criteriul III, obtinem
si,
dupa criteriul III, obtinem
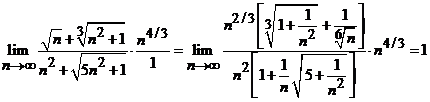 .
.
Deci, cele doua serii au aceeasi natura si anume sunt convergente.
Seria 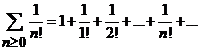 , este convergenta si are suma egala cu
, este convergenta si are suma egala cu ![]() .
.
Aratati ca seria 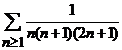 este
convergenta si are suma egala cu
este
convergenta si are suma egala cu ![]() .
.
Exercitii propuse
(a). Studiati natura urmatoarelor serii :
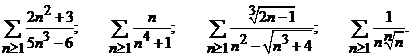 .
.
(b). Determinati suma seriei ![]()
Indicatie. Putem scrie
identitatea ![]() unde, prin identificare, gasim
unde, prin identificare, gasim ![]() si
si ![]() . Atunci termenul general al seriei devine
. Atunci termenul general al seriei devine
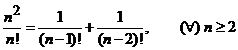
si, prin urmare,
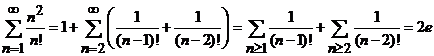 .
.
(c). Se considera seriile numerice
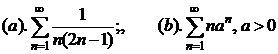 (discutie
dupa valorile lui
(discutie
dupa valorile lui ![]() ).
).
i). Studiati convergenta seriilor (folosind criteriile cunoscute pentru serii cu termeni pozitivi; enuntati aceste criterii) .
ii). In cazul convergentei sa se calculeze suma seriilor.
(d). Studiati natura seriei ![]() .
.
Solutie. Daca ![]() atunci obtinem seria armonica
atunci obtinem seria armonica ![]() .
.
In inegalitatea evidenta
![]() , (1.1)
, (1.1)
daca substituim,
succesiv, ![]() obtinem ca
subsirul
obtinem ca
subsirul ![]() al sirului
sumelor partiale
al sirului
sumelor partiale![]() , este nemarginit superior:
, este nemarginit superior:
![]() .
.
Asadar, sirul sumelor partiale are limita infinita si deci, seria este divergenta.
Observatie. Inegalitatea (1.1) arata ca sirul sumelor partiale
asociat seriei nu este sir Cauchy. Intr-adevar, daca alegem ![]() , deducem
, deducem
![]() , pentru orice
, pentru orice ![]()
si atunci din criteriul general al lui Cauchy obtinem ca seria este divergenta.
Daca ![]() atunci termenii
corespunzatori ai seriei considerate sunt mai mari decat termenii seriei
armonice (divergenta). Potrivit criteriului I de comparatie
rezulta ca seria
atunci termenii
corespunzatori ai seriei considerate sunt mai mari decat termenii seriei
armonice (divergenta). Potrivit criteriului I de comparatie
rezulta ca seria ![]() , este divergenta.
, este divergenta.
Daca ![]() , vom pune
, vom pune ![]() , unde
, unde ![]() . Analog inegalitatii (1.1), avem inegalitatea
. Analog inegalitatii (1.1), avem inegalitatea
![]() , (1.2)
, (1.2)
Procedand ca mai sus, obtinem
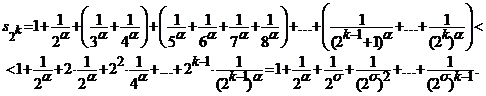
Rezulta ca sumele partiale ale seriei considerate sunt majorate de numarul constant
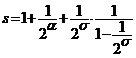
si deci, seria este convergenta.
(e). Fie seria 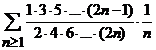 . Utilizand unul din criteriile de convergenta
studiate, aratati ca seria este convergenta.
. Utilizand unul din criteriile de convergenta
studiate, aratati ca seria este convergenta.
Solutie. Notam cu ![]() termenul general al
seriei date. Din criteriul raportului, deducem
termenul general al
seriei date. Din criteriul raportului, deducem
![]() .
.
Prin urmare, cu criteriul raportului, nu putem decide natura seriei. Vom aplica, in continuare, criteriul lui Raabe si Duhamel.
Avem
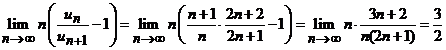 .
.
Deci,
seria ![]() este convergenta.
este convergenta.
f). Calculati suma urmatoarelor serii :
). 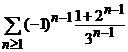 . R. Seria este
convergenta si are suma egala cu
. R. Seria este
convergenta si are suma egala cu ![]() .
.
![]() . R. Sirul
sumelor partiale este
. R. Sirul
sumelor partiale este ![]() este convergent
si avem
este convergent
si avem ![]() (unde
(unde ![]() se numeste constanta
lui Euler).
se numeste constanta
lui Euler).
). ![]() .
.
Solutie. Termenul general al
seriei are forma ![]() .
.
Atunci 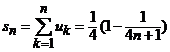 si deci, suma
seriei este egala cu
si deci, suma
seriei este egala cu ![]() .
.
). 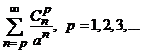 si
si ![]() . ( unde,
. ( unde, ![]() ) .
) .
Solutie. Deoarece 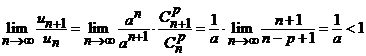 , atunci, din criteriul raportului, deducem ca seria
este convergenta. Fie sirul sumelor partiale
, atunci, din criteriul raportului, deducem ca seria
este convergenta. Fie sirul sumelor partiale 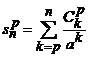 ,
, ![]() si
si 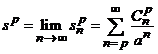 , suma seriei. Folosind relatia de recurenta
, suma seriei. Folosind relatia de recurenta ![]() , putem scrie
, putem scrie 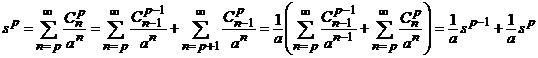 .
.
Asadar, avem ![]() , oricare ar fi
, oricare ar fi ![]() Folosind aceste
relatii de recurenta, obtinem
Folosind aceste
relatii de recurenta, obtinem
![]() ,
,
unde
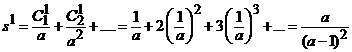 .
.
In consecinta,
seria are suma egala cu ![]() .
.
Exercitii
). Aratati ca seria ![]() este convergenta
si determinati suma sa.
este convergenta
si determinati suma sa.
R.
Folosind identitatea ![]() , deducem ca seria este convergenta si are
suma egala cu
, deducem ca seria este convergenta si are
suma egala cu ![]() .
.
). Studiati natura seriei ![]() . R. Fie
. R. Fie ![]() termenul general al
seriei. Deoarece
termenul general al
seriei. Deoarece ![]() , atunci seria este divergenta.
, atunci seria este divergenta.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |