SIRURI
I. DEFINITIE
Se numeste
sir de numere reale o functie definita pe ![]() cu valori in
cu valori in ![]() ,
, ![]() sirul se
noteaza
sirul se
noteaza ![]() ;
; ![]() se numeste termenul de rangul
se numeste termenul de rangul ![]() al sirului
al sirului
Observatii Un sir se poate descrie:
a)
printr-o
regula de calcul - exprimare analitica: ![]()
b)
prin mai multe
reguli de calcul: 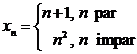
c)
printr-o
relatie de recurenta: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
II. DEFINITIE
Spunem ca l (finit sau infinit)
este limita sirului ![]() si scriem
si scriem ![]() , daca in afara oricarei vecinatati
a lui l se afla, cel mult, un numar finit de termeni ai sirului.
, daca in afara oricarei vecinatati
a lui l se afla, cel mult, un numar finit de termeni ai sirului.
Spunem ca
sirul este convergent daca are limita finita ![]()
III. SIRURI MARGINITE
Se spune ca sirul ![]() este marginit
superior (majorat) daca exista
este marginit
superior (majorat) daca exista ![]() astfel incat
astfel incat ![]() ,
, ![]()
Se spune ca
sirul ![]() este marginit inferior (minorat)
daca exista
este marginit inferior (minorat)
daca exista ![]() astfel incat
astfel incat ![]() ,
, ![]()
Se spune ca
sirul ![]() este marginit daca
este marginit daca ![]() numerele reale
numerele reale ![]() astfel incat
astfel incat ![]() ,
, ![]()
![]()
Sirul ![]() este marginit
este marginit ![]() astfel incat
astfel incat ![]() ,
, ![]()
Un sir care nu este marginit se numeste nemarginit.
IV. SIRURI MONOTONE
Se numeste
sir strict crescator daca: ![]() ,
, ![]() adica:
adica:
![]()
Se numeste
sir strict descrescator daca: ![]() ,
, ![]() adica:
adica:
![]()
Se spune ca sirul ![]() este:
este:
a)
crescator daca ![]()
![]() adica daca
adica daca ![]()
b)
descrescator
daca ![]() ,
, ![]() adica daca
adica daca ![]()
Pentru a stabili monotonia unui
sir se calculeaza diferenta a doi termeni consecutivi oarecare ![]() sau in cazul in
care termenii sunt pozitivi se face catul a doi termeni consecutivi
sau in cazul in
care termenii sunt pozitivi se face catul a doi termeni consecutivi ![]() .
.
V. SIRURI CONVERGENTE
Teorema de convergenta cu ![]() :
: ![]() sau
sau ![]() ,
,![]()
![]()
![]() ,
,![]()
astfel incat ![]()
![]() ,
, ![]() .
.
Teorema de convergenta cu
![]() : Orice subsir al
uni sir convergent este de ase-
: Orice subsir al
uni sir convergent este de ase-
menea convergent si are aceeasi limita.
Obsevatie Subsirul ![]() se numeste sir extras din sirul
se numeste sir extras din sirul
![]() .
.
Teorema lui Bolzano-Weierstrass: Din orice sir
marginit ![]() se poate extrage
se poate extrage
un subsir ![]() convergent.
convergent.
Teorema sirului fundamental (sir Cauchy): Un sir ![]() se numeste sir
se numeste sir
fundamental daca![]()
![]()
![]() ,
,![]() astfel incat
astfel incat ![]()
![]() pentru
pentru ![]() si
si ![]() oarecare.
oarecare.
Observatii
a) Un sir de numere reale este convergent daca si numai daca este sir Cauchy.
b) Orice sir monoton si marginit este convergent ( teorema Weierstrass ).
VI. PROPRIETATILE LIMITEI UNUI SIR
Un sir convergent are o singura limita.
Prin adaugarea sau inlaturarea unui numar finit de termeni, un sir convergent
ramane convergent catre aceeasi limita.
VII. CRITERIUL MAJORARII
Teorema Daca ![]() ,
, ![]() si
si ![]() , atunci
, atunci ![]()
Corolar 1: Daca ![]() ,
, ![]() si
si ![]() atunci
atunci ![]()
Corolar 2: Daca ![]() ,
, ![]() si
si ![]() atunci
atunci ![]()
Corolar 3: Daca ![]() ,
, ![]() (
( ![]() fixat ),
fixat ), ![]() atunci
atunci ![]()
Corolar 4: Daca ![]() ,
, ![]()
![]() fixat ),
fixat ), ![]() atunci
atunci ![]()
VIII. TRECEREA LA LIMITA IN INEGALITATI
Teorema: Daca ![]() si
si ![]() sunt siruri
convergente si daca
sunt siruri
convergente si daca ![]() ,
, ![]()
![]() fixat ), atunci
fixat ), atunci ![]()
IX. TEOREMA " CLESTELUI "
Fie ![]() ,
, ![]() ,
, ![]() trei siruri satisfacand
conditiile:
trei siruri satisfacand
conditiile:
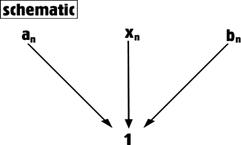
a)
![]() ,
, ![]()
b)
![]() atunci sirul
atunci sirul ![]() este convergent si
este convergent si ![]() .
.
X. CRITERIUL RAPORTULUI
Forma cu inegalitati
Fie ![]() un sir de numere strict pozitive:
un sir de numere strict pozitive:
a)
Daca ![]()
![]()
![]() astfel incat
astfel incat 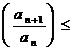
![]() ,
, ![]() atunci sirul este conver-
atunci sirul este conver-
gent si ![]() .
.
b)
Daca ![]()
![]()
![]() astfel incat
astfel incat 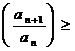
![]() ,
, ![]() , atunci sirul este di-
, atunci sirul este di-
vergent si ![]()
Forma la limita
Fie ![]() un sir de numere strict pozitive;
presupunem ca exista
un sir de numere strict pozitive;
presupunem ca exista 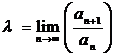 . Atunci:
. Atunci:
a)
Daca ![]()
![]()
![]()
b)
Daca ![]()
![]()
![]()
XI. LEMA LUI STOLTZ
Fie ![]() ,
, ![]() doua siruri
de numere reale satisfacand conditiile:
doua siruri
de numere reale satisfacand conditiile:
a)
Sirul ![]() este strict pozitiv, strict crescator
si nemarginit.
este strict pozitiv, strict crescator
si nemarginit.
b)
Exista ![]() . Atunci exista limita raportului
. Atunci exista limita raportului ![]() si avem:
si avem:
![]()
Consecinte:
a)
Fie ![]() un sir de numere reale care
are limita. Atunci:
un sir de numere reale care
are limita. Atunci:
![]()
b)
Fie ![]() un sir de numere pozitive care
are limita. Atunci:
un sir de numere pozitive care
are limita. Atunci:
![]()
c)
Fie ![]() un sir de numere strict pozitive.
Daca sirul
un sir de numere strict pozitive.
Daca sirul 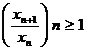 are
are
limita,
atunci: ![]() .
.
XII. SIRURI TIP
Sirul cu termenul general ![]() unde
unde ![]() :
: 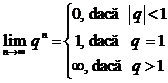
Observatie: Nu exista limita daca
![]()
Sirul ![]() cu functie
reala polinomiala:
cu functie
reala polinomiala: ![]() ;
;
grad![]() ;
; ![]() :
: 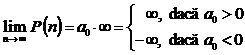
Sirul ![]() cu
cu ![]() functii reale polinomiale:
functii reale polinomiale: ![]()
grad![]() ;
; ![]() ;
; ![]() ; grad
; grad ![]() ;
; ![]() ;
;
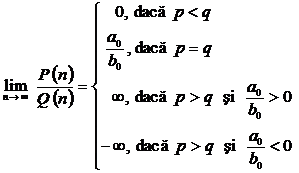
Siruri care au
ca limita numarul ![]()
Se arata ca:
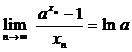 , daca
, daca ![]() si
si ![]() , daca
, daca ![]()
![]() , daca
, daca ![]() si
si ![]() , daca
, daca ![]()
a)
![]() ; b)
; b) 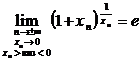 ;
;
c)
Suma unei progresii geometrice: daca ![]() atunci:
atunci:
![]()
XIII. SIRURI REMARCABILE
Numarul ![]()
Sirul cu termenul general 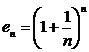 este strict
crescator si marginit
este strict
crescator si marginit ![]()
Se noteaza 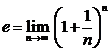 ,
, ![]() si exista inegalitatea
si exista inegalitatea ![]()
Sirul ![]() are ca limita tot numarul
are ca limita tot numarul ![]() ; Avem
; Avem ![]()
Constanta lui Euler
Sirul cu termenul general ![]() ,
, ![]() este strict descrescator si minorat
de zero; limita sa
este strict descrescator si minorat
de zero; limita sa ![]() si exista inegalitatea:
si exista inegalitatea: ![]()
Sirul lui Fibonacci
Este definit de recurenta: ![]() ,
, ![]()
Termenul general se scrie: 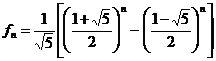 si are proprietatea:
si are proprietatea:
![]()
Sirul lui Traian Lalescu :
Este definit prin termenul general:
![]()
![]()
Sirul lui Newton :
Este definit
prin recurenta 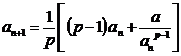 unde
unde ![]() si are proprietatea
si are proprietatea ![]() .
.
XIV. SIRURI RECURENTE
Un sir ![]() se numeste sir recurent de ordinul
se numeste sir recurent de ordinul ![]() (
( ![]() dat ), daca este definit de o
relatie de forma
dat ), daca este definit de o
relatie de forma ![]() ,
, ![]() cu
cu ![]() numere date.
numere date.
Recurenta liniara de ordinul
doi, omogena cu coeficienti, sunt de forma ![]() ,
, ![]() cu
cu ![]() numere date.
numere date.
Acestei recurente i se
asociaza ecuatia caracteristica in ![]()
![]()
Pentru explicarea termenului ![]() se considera cazurile:
se considera cazurile:
a)
![]() solutiile generale
solutiile generale ![]()
b)
![]()
c)
![]()
Observatii:
Numerele A si
B se determina in functie de ![]() date.
date.
Pentru o recurenta liniara si neomogena, solutia generala se obtine din solutia
generala a recurentei omogene atasate, la care se adauga o solutie particulara a celei neomogene.
Relatii
liniare de recurenta (ordinul intai): 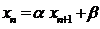 unde
unde ![]() se determina
se determina
folosind algoritmul de adunare al termenilor.
XV. OPERATII CU SIRURI CONVERGENTE
Fie ![]() doua siruri. Daca
doua siruri. Daca ![]() ,
, ![]() ,
, ![]() atunci:
atunci:
a)
![]() este convergent si
este convergent si ![]() ( limita sumei
( limita sumei
este egala cu suma limitelor )
b)
![]() este convergent
si
este convergent
si ![]() (o
(o
limitei )
c)
![]() este convergent
si
este convergent
si ![]() (limita produ-
(limita produ-
sului este egala cu produsul limitelor ).
d)
![]() este convergent
si
este convergent
si 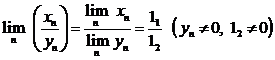 ( limita catului
( limita catului
este egala cu catul limitelor )
e)
![]() este convergent
si
este convergent
si ![]() ( limita modulului
este egala cu mo-
( limita modulului
este egala cu mo-
dulul limitei )
XVI. TEOREMA DE CONVERGENTA
Orice sir
monoton crescator si marginit superior de numere reale ( in ![]() ) este
) este
convergent.
Orice sir
monoton descrescator si marginit inferior in ![]() este convergent.
este convergent.
XVII. ALTE OPERATII CU SIRURI CONVERGENTE
Limita unei puteri se distribuie si bazei si exponentului:
![]()
Limita radicalului este egala cu radicalul limitei:
![]() ,
, ![]() ,
, ![]()
Limita logaritmului este egala cu logaritmul limitei:
![]()
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |