Teorema lui CASEY

Definitie : Fiind date doua cercuri C(O₁,r₁) si C(O₂,r₂) de centre O₁,O₂ si raze r₁, r₂ , numim distanta tangentiala intre cele doua cercuri (si notam cu d(O₁,O₂) lungimea tangentei comune exterioare duse la cele doua cercuri (lungimea segmentului cuprins intre cele doua puncte de tangenta)

Teorema lui CASEY : Fie C(O, r), C(O₁,r₁), C(O₂,r₂), C(O₃,r₃) si   C(O₄,r₄) cinci cercuri de centre O, O₁, O₂, O₃, O₄ si raze r, r₁, r₂, r₃, r₄. Daca cercurile C , C C si C sunt tangente interior la cercul C (presupunem orientarea in ordinea numerotarii), atunci avem urmatoarea relatie intre distantele tangentiale dintre cercuri:

d(O₁,O₂)* d(O₃,O₄)+ d(O₂,O₃)* d(O₄,O₁)= d(O₁,O₃)* d(O₂,O₄)

Rezultatul este valabil si in cazul in care cercurile sunt tangente exterior.

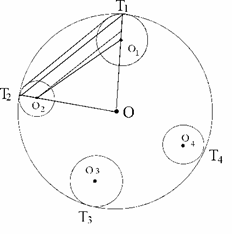
Demonstratie: Sa notam cu T₁, T₂, T₃, T₄ punctele de tangenta ale cercurilor C , C C si respectiv C cu cercul C si sa exprimam distanta tangentiala d(O_i,O_j) dintre doua cercuri C_i C_j in functia de razele cercurilor r_i, r_j, raza r a cercului C(O,r si distanta T_iT_j dintre punctele de tangenta cu C(O,r