Definitie Tetraedrul [ABCD] se numeste dreptunghic in A daca oricare doua din muchiile [AB], [AC], [AD] sunt perpendiculare .
Se observa usor ca un tetraedru dreptunghic este si ortocentric , deci are proprietatile mentionate in paragraful 3.1.2. Se va constata insa ca aceste tetraedre au si proprietati suplimentare ce generalizeaza intr-un mod remarcabil relatiile metrice din triunghiul dreptunghic.
Teorema 41:
Daca tetraedrul [ABCD] este dreptunghic in A si proiectia ortogonala a lui A in planul (BCD) este H, atunci este ortocentrul triunghiului ascutitunghic [BCD].
 Demonstratie :
Demonstratie :
![]() AB AD
AB AD
TAB CD
BD AC
AH ( BCD) T AH CD
![]() CD AB
CD AB
T CD (ABH) T CD BH
CD AH
Deci AH este inaltime dusa din B a triunghiului [BCD]. Analog se arata CH si DH sunt inaltimile din C , respectiv D ale DBCD.
In D BAC: m(![]() ) = 90o , AE BC T E I BC.
) = 90o , AE BC T E I BC.
In D DAE: m(![]() ) = 90o , AH DE T H I DE.
) = 90o , AH DE T H I DE.
Deducem ca H I Int(BCD) , adica triunghiul [BCD] este ascutitunghic.
Observatie :
Pentru demonstrarea faptului ca fata opusa triedrului drept este triunghi ascutitunghic mai putem proceda si astfel:
Notam cu x,y,z lungimile muchiilor [AB], [AC], [AD] si cu b,c,d lungimile laturilor triunghiului [BCD].
![]()
![]()
![]() x2 +y2 =d2
x2 +y2 =d2 ![]()
![]()
x2 +z2
=c2 ![]()
![]()
y2 +
z2=b2 ![]()
![]()
Cum x>0, y>0, z>0 expresiile de sub radical exista in R si sunt pozitive, deci b2 < c2 +d2, c2 < b2 +d2, d2 < b2 +c2, relatii ce caracterizeaza laturi ce se opun la unghiuri ascutite in triunghi.
Teorema 42:
In tetraedrul [ABCD] dreptunghic in A are loc relatia (SABCD)2 = SDBC SHBC.
 Demonstratie :
Demonstratie :
In DAED dreptunghic in A aplicam teorema catetei T
AE2 = ED EH
Inmultim aceasta relatie cu BC2 si rezulta
(AE2 BC2) = (ED BC) ( EH BC)
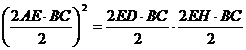
![]() 4(SABC)2=
2SBCD 2 SHBC. Deci (SABC)2=
SBCD SHBC.
4(SABC)2=
2SBCD 2 SHBC. Deci (SABC)2=
SBCD SHBC.
![]() Teorema 43:
Teorema 43:
In tetraedrul [ABCD] dreptunghic in A are loc relatia S2ABC + S2ACD + S2ABD = S2BCD.
Demonstratie :
Folosim teorema 42 : S2ABC = SBCD SBCH
S2ACD = SBCD SCDH
S2ABD = SBCD SBDH.
Adunand aceste relatii obtinem S2ABC + S2ACD + S2ABD = SBCD ( SBCH + SCDH + SBDH); H I Int(BCD). Deci S2ABC + S2ACD + S2ABD = S2BCD.
Teorema 44:
[ABCD] este un tetraedru dreptunghic in A faca si numai daca au loc egalitatile :
2AB2= d2 + c2 - b2 ; 2AC2= d2 + b2 - c2 ; 2AD2= b2 + c2 - d2; unde CD=b, BD=c, BC=d.
Demonstratie :
Intr-adevar , daca [BCDA] este tridreptunghic in A , aplicam teorema lui Pitagora si avem

![]() AB2 + AC2
=d2
AB2 + AC2
=d2
AC2 + AD2 =b2
AD2 + AB2 =c2 .
Rezolvand sistemul se obtine:
![]() 2AB2 =d2
+ c2 - b2
2AB2 =d2
+ c2 - b2
2AC2 = d2 + b2 - c2
2AD2= b2 + c2 - d2.
Reciproc: egalitatile din enunt asigura relatiile sistemului si prin reciproca teoremei lui Pitagora , rezulta ca unghiurile plane ale tetraedrului in A sunt drepte.
Teorema 45:
Fie un tetraedru ortocentric [ABCD] , H ortocentrul sau, O centrul sferei circumscrise , I centrul sferei inscrise. Urmatoarele propozitii sunt echivalente:
P1: Punctele D,H,O sunt coliniare
P2: Punctele D,I,H sunt coliniare
P3: Tetraedrul [ABCD] este dreptunghic in D sau izofacial de baza [ABC] ( piramida triunghiulara regulata de baza [ABC]).
Vom folosi urmatoare schema : (P1) (P3) (P2).
Demonstratie :
(P1) T (P2) .
Daca punctele D si H coincid atunci [ABCD] este evident dreptunghic in D , deci are loc P3. Daca D H , dreapta DH fiind perpendiculara pe (ABC) si continand O cu proprietatea [OA]s[OB]s[OC] , coincide cu dreapta mediatoare a triunghiului [ABC]. Rezulta [DA]s[DB]s[DC] . Apoi punctul E comun lui (DH) si ( ABC) este si ortocentru si centru al cercului circumscris lui [ABC], deci DABC echilateral.
 (P2) T (P3)
.
(P2) T (P3)
.
Daca D =H se deduce P3 ca in etapa precedenta.
Daca D H , dreapta DH contine pe I , egal departat de
fetele tetraedrului D(ABC) deci coincide cu bisectoarea
acestui triedru.
Fie FI(DH) (ABC). Deoarece H este ortocentrul tetraedrului,
F este ortocentrul DABC. Fie M,N,P proiectiile ortogonale ale
lui F pe dreptele BC, CA, AB. Conform teoremei celor trei perpendiculare proiectiile ortogonale M , N ,P ale lui F in planele Af, Bf, Cf sunt pe dreptele DM,DN, DP.
Din
[FM s[FN s[FP ] urmeaza ![]() s
s![]() s
s![]() , deci [FM]s[FN]s[FP].
, deci [FM]s[FN]s[FP].
Rezulta ca F este si centrul cercului inscris in DABC, deci DABC este echilateral si M, N,P sunt mijloacele laturilor sale. In triunghiurile [BDC];[DCA] ; [DAB],medianele din D sunt si inaltimi, deci aceste triunghiuri sunt isoscele. Deci [DA]s[DB]s[DC] si prin urmare [ABCD] este izofacial
P3TP1 P2
Daca tetraedrul [ABCD] este dreptunghic , atunci D=H si proprietatile P1,P2 sunt evidente.
Daca D H ,atunci perpendiculara din D pe (ABC) contine evident H. Din [DA]s[DB]s[DC] rezulta ca DH este mediatoarea corespunzatoare triunghiului[ABC] , deci contine O, deci are loc P1. Dreapta DH contine centrul de greutate al triunghiului [ABC], punct ce coincide cu centrul cercului inscris in triunghi.
Considerand deci M,N,P mijloacele laturilor [BC], [CA],[AB] urmeaza ca triunghiurile dreptunghice [DGM];[DGN]; [DGP] sunt congruente , deci au si inaltimile congruente. Deci [DG este bisectoarea triedrului D(ABC) si contine I.
S-a dedus astfel si proprietatea P2.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |