
Actiunea fluidelor vascoase asupra corpurilor solide
Folosind (4.8)1 si (11.1), expresia tensiunii intr-un fluid newtonian capata forma
![]() . (11.110)
. (11.110)
Fie S o suprafata in repaus la care fludul vascos adera, v = 0 pe S (v. figura 11.19); din (2.27)1 si (2.27)3 se obtin urmatoarele conditii cinematice pe S
![]() , (11.111)
, (11.111)
![]() , (11.112)
, (11.112)
unde ![]() este vectorul vartej.
este vectorul vartej.
Fig. 11.19. Distributia de viteze in vecinatatea
unei suprafete la care fluidul vascos adera.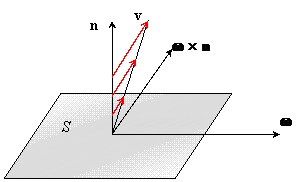

Din (11.112) si (11.110) rezulta expresia tensiunii pe o suprafata in repaus la care fluidul adera,
![]() , (11.113)
, (11.113)
relatia (11.113) fiind echivalenta cu
![]() , (11.114)
, (11.114)
unde ![]() reprezinta
derivata vitezei dupa directia normalei in punctul respectiv .
reprezinta
derivata vitezei dupa directia normalei in punctul respectiv .
Forta cu care fluidul actioneaza asupra unui corp are deci expresia
![]() . (11.115)
. (11.115)
Tensiunea t pe suprafata corpului se poate
descompune intr-o componenta normala ![]() , egala cu presiunea pn pentru un fluid newtonian
incompresibil, si o componenta tangentiala
, egala cu presiunea pn pentru un fluid newtonian
incompresibil, si o componenta tangentiala ![]() , direct proportionala cu viscozitatea (v. figurile
11.20 si 4.3). In concluzie,
daca se cunoaste distributia de presiuni si vartej pe
suprafata corpului se poate determina, folosind (11.113) si (11.115),
actiunea fluidului in miscare asupra corpurilor si
suprafetelor solide cu care vine in contact.
, direct proportionala cu viscozitatea (v. figurile
11.20 si 4.3). In concluzie,
daca se cunoaste distributia de presiuni si vartej pe
suprafata corpului se poate determina, folosind (11.113) si (11.115),
actiunea fluidului in miscare asupra corpurilor si
suprafetelor solide cu care vine in contact.
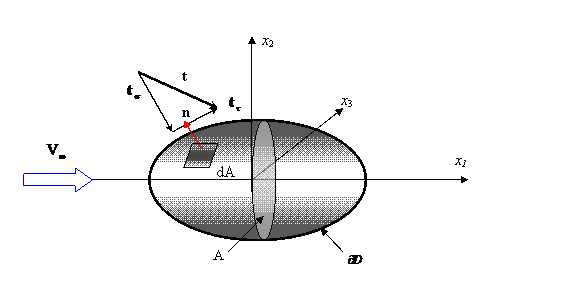
Fig. 11. 20. Actiunea
unui curent de fluid cu viteza ![]() asupra unui corp solid
asupra unui corp solid
Se
considera un corp solid aflat intr-un curent de fluid infinit in camp
gravitational, viteza fluidului neperturbat de prezenta corpului
solid fiind ![]() (directia
vitezei
(directia
vitezei ![]() determinand
directia axei Ox1). Opusul
proiectiei fortei R pe
directia axei 0x1,
respectiv
determinand
directia axei Ox1). Opusul
proiectiei fortei R pe
directia axei 0x1,
respectiv
![]() (11.116)
(11.116)
poarta denumirea de
forta de rezistenta la inaintare; A (denumita si "aria
maestra") reprezinta aria maxima obtinuta prin
sectionarea corpului cu un plan perpendicular pe ![]()
In (11.116) Cx reprezinta coeficientul de rezistenta la inaintare, acesta fiind functie de numarul Reynolds caracteristic curgerii, de forma geometrica a corpului si de geometria locala a suprafetei corpului, respectiv rugozitatea suprafetei (pentru detalii vezi Ionescu ). Coeficientul de rezistenta la inaintare reprezinta o caracteristica importanta a corpurilor hidro- si aerodinamice (pale de masini hidraulice, profile aerodinamice etc.). In majoritatea cazurilor, Cx se detemina experimental sau numeric (prin integrarea directa a ecuatiei Navier-Stokes si obtinerea distributiei de eforturi pe suprafata corpului).
Un caz clasic de calcul analitic al coeficientului Cx este miscarea in aproximatia Stokes (Re << 1) in jurul unei sfere aflata intr-un curent de fluid infinit, miscarea fiind considerata cu simetrie axiala (v. figura 11.21).
In aceasta ipoteza, expresiile functiei de curent, a distributiei de viteze si vartej in jurul sferei sunt urmatoarele (v. referinta 7):
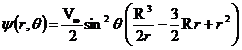 ; (11.117)
; (11.117)
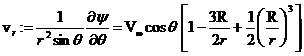 , (11.118)
, (11.118)
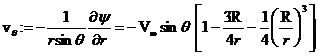 , (11.119)
, (11.119)
![]() ; (11.120)
; (11.120)
pe sfera distributia de presiuni fiind data de
![]() . (11.121)
. (11.121)
Deoarece ![]() , tensiunea (11.113) pe suprafata sferei are expresia
, tensiunea (11.113) pe suprafata sferei are expresia
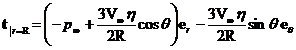 ; (11.122)
; (11.122)
din (11.115) rezultand
![]()
cu ![]() .
.
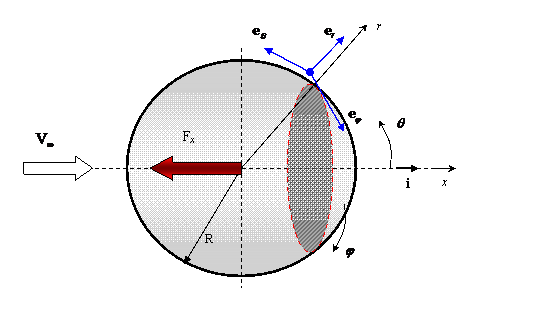
Fig. 11. 21. Geometria miscarii in jurul unei sfere
Datorita simetriei corpului, prima integrala din (11.123) este nula, deci
![]() (11.124)
(11.124)
respectiv
![]() . (11.125)
. (11.125)
Din (11.125) si (11.116), cu ![]() , se obtine expresia coeficientului de
rezitenta la inaintare
, se obtine expresia coeficientului de
rezitenta la inaintare
![]() , (11.126)
, (11.126)
unde ![]() , cu d = 2R
diametrul sferei.
, cu d = 2R
diametrul sferei.
Expresia (11.125) este valabila la numere Reynolds foarte mici, Re << 1. La numere Reynolds mici, Re < 2, Oseen a obtinut expresia (v. referinta7)
![]() . (11.127)
. (11.127)
Caderea
unei sfere intr-un fluid vascos este o problema indelung studiata in
mecanica fluidelor datorita aplicatiilor practice, de exemplu,
masurarea viscozitatii cu viscozimetrul Höppler. In acest caz,
bila cu diametrul d cade liber intr-un tub cu diametrul D, plin cu fluidul a carui
viscozitate dorim sa o calculam. Din echilibrul fortelor de rezisntenta
la inaintare Fx, fortei de
greutate G si
fortei arhimedice, prin masurarea vitezei de cadere a bilei in
fluidul vascos w denumita
si marime hidraulica, cu ![]() in (11.125) se obtine valoarea coeficientului de
viscozitate
in (11.125) se obtine valoarea coeficientului de
viscozitate ![]() . Evident, in acest caz miscarea bilei nu se face
intr-un spatiu infinit; in general se admite ca expresia fortei
de rezistenta la inaintare are expresia
. Evident, in acest caz miscarea bilei nu se face
intr-un spatiu infinit; in general se admite ca expresia fortei
de rezistenta la inaintare are expresia
![]() , (11.128) unde functia
, (11.128) unde functia ![]() ,
, ![]() daca
daca ![]() si Re << 1, se
determina experimental sau numeric19
(expresia fortei de rezistenta la inaintare devine mult mai complicata
daca miscarea sferei nu este simetrica in tubul cu diametrul D).
si Re << 1, se
determina experimental sau numeric19
(expresia fortei de rezistenta la inaintare devine mult mai complicata
daca miscarea sferei nu este simetrica in tubul cu diametrul D).
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |