Algebre si morfisme
Pentru o
multime nevida A si un numar natural n definim A° = iar pentru n > 0, 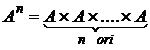
Definitia 1.1. Prin operatie algebrica n - ara pe multimea A intelegem o aplicatie f : An A. (n va purta numele de rangul lui f ).
O operatie f : A° = A se zice operatie nula, f : A A se zice operatie unara, f : A![]() A se zice operatie binara.
A se zice operatie binara.
Prin tip de similitudine (sau simplu tip) intelegem un m - uplu de numere naturale, t = (n1 , n2 , nm) (m se va numi ordinul lui t si vom scrie m = 0 (t
Prin algebra de tipul t = (n1 ,n2 , n0(t ) intelegem o pereche A = (A , F) unde A este o multime nevida (numita universul algebrei A) iar F este un 0 (t) - uplu de operatii pe A ( f1 , f2 , ,f0 (t ) astfel incat pentru 1 i t), fi este operatie ni - ara pe A.
Observatie
. De obicei pentru toate algebrele de acelasi tip t vom folosi aceeasi notatie fi pentru operatia ni - ara, 1 i t
. Prin algebra vom intelege doar universul sau (fara a mai specifica de fiecare data operatiile) iar cand vorbim in general de o algebra de tip t vom intelege o algebra A de tipul (n1, n 2, , n0 ( t
. A da o operatie nula pe A revine de fapt la a pune in evidenta un element al lui A.
Definitia 1.2. O algebra A = (A, F) se zice unara daca toate operatiile sale sunt unare si monounara daca are o singura operatie unara.
A se zice grupoid daca are o singura operatie binara, finita daca A este multime finita si triviala daca A are un singur element.
. Grupurile. Un grup este o algebra (G , , -1 , 1) cu o operatie binara ' ', una unara ' ![]() '
si alta nula 1 I G astfel incat sa fie verificate identitatile:
'
si alta nula 1 I G astfel incat sa fie verificate identitatile:
G![]() : x (y z) = (x y) z
: x (y z) = (x y) z
G![]() : x x =
x
: x x =
x
G![]() : x x -1
= x -1 x =
1
: x x -1
= x -1 x =
1
Un grup se zice comutativ (sau abelian) daca mai verifica in plus si identitatea:
G![]() : x · y = y · x
: x · y = y · x
. Semigrupurile si monoizii. Prin semigrup intelegem un grupoid in care (G1) este verificata iar prin monoid o algebra (M , , 1) cu o operatie binara ' ' si una nula 1 I M astfel incat (G1) si (G2) sunt verificate.
. Inelele. Un inel este o algebra (A , + , , - , 0) unde ' + ' si ' ' sunt operatii binare pe A, ' - ' este o operatie unara iar 0 I A este o operatie nula astfel incat:
A![]() : (A , + , - , 0 )
este un grup abelian
: (A , + , - , 0 )
este un grup abelian
A![]() : (A , ) este semigrup
: (A , ) este semigrup
A![]() : Sunt verificate identitatile:
: Sunt verificate identitatile:
x (y + z) = x y + x z
(x + y) z = x z + y z
Prin inel unitar intelegem o algebra (A, +, , - , 0, 1) astfel incat (A, + , , - ,0) este un inel, 1I A este o operatie nula astfel incat (G2) este verificata.
. Semilatici. Din punct de vedere al algebrei universale, prin semilatice intelegem un semigrup (S , ) ce satisface pe (G4) si legea de idempotenta:
S1: x x = x
Latici. Din punct de vedere al algebrei universale, prin latice intelegem o algebra (L, ) cu doua operatii binare si astfel incat sunt verificate identitatile:
L1: Legea de comutativitate:
(a) x y = y x
(b) x y = y x
L2 : Legea de asociativitate:
(a) ( x y ) z = x ( y z )
(b) (x y ) z = x ( y z )
L3 : Legea de idempotenta:
(a) x x = x
(b) x x = x
L 4 : Legea de absorbtie:
(a) x ( x y ) = x
(b) x ( x y ) = x
O latice marginita este o algebra (L , , , 0 , 1) astfel incat (L , ) este latice, 0, 1 I L sunt operatii nule astfel incat sunt verificate identitatile:
x
x
Definitia 1.3. Fie A si B doua algebre de acelasi tip t O aplicatie f : A B se zice morfism de algebre de tip
t (sau simplu morfism) daca pentru
orice 1 i t) si a![]() , a
, a![]() , , a
, , a![]() I An
I An![]() avem: f(fi( a1 , a2 ,
,a
avem: f(fi( a1 , a2 ,
,a![]() )) = fi(f(a1) , , f (a
)) = fi(f(a1) , , f (a![]() )).
)).
Exemple:
1. Cvasigrupurile si loop-urile
Un cvasigrup este o algebra ![]() impreuna
cu trei operatii binare care satisface urmatoarele
identitati
impreuna
cu trei operatii binare care satisface urmatoarele
identitati
Q1: x (x · y)![]() y
y
(x · y) / y![]() x
x
Q2: x ·(x y)![]() y
y
(x / y) · y![]() x
x
Un loop este un cvasigrup impreuna cu identitatea, i.e., o algebra ![]() care satisface (Q1), (Q2) si (G2).
care satisface (Q1), (Q2) si (G2).
Module peste un inel fix
Fie R
dat ca inel. Un R-modul (stang) este
o algebra ![]() unde "+" este binara, "-" este
unara, "0" este nula, si fiecare fr este unara,
astfel ca urmatoarele au loc:
unde "+" este binara, "-" este
unara, "0" este nula, si fiecare fr este unara,
astfel ca urmatoarele au loc:
M1: ![]() este un grup abelian
este un grup abelian
M2: fr(x+y) fr(x) + fr(y), pentru rIR
M3: fr+s(x) fr(x) + fs(x), pentru r, s I R
M4: fr(fs(x)) frs(x), pentru r, s I R.
Fie R dat ca inel cu identitatea. Un R-modul unitar este o algebra care ca mai sus satisface (M1)- (M4) si
M5: f1(x) x.
Algebre peste un inel
Fie R
dat ca inel impreuna cu identitatea. O algebra
peste R este o algebra ![]() astfel ca au loc urmatoarele:
astfel ca au loc urmatoarele:
A1: ![]() este un R-modul unitar
este un R-modul unitar
A2: ![]() este un inel
este un inel
A3: fr(xy) (fr(x)) · y x · fr(y) pentru rIR
4. Algebre Boole
O algebra
Boole este o algebra 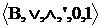 impreuna cu
doua operatii binare, o operatie unara si doua
operatii nule care satisfac:
impreuna cu
doua operatii binare, o operatie unara si doua
operatii nule care satisfac:
B1: ![]() este o latice
distributiva
este o latice
distributiva
B2: x
x
B3: x x![]()
x x![]()
Algebrele Boole au fost descoperite ca rezultat al investigatilor Boole de la baza legilor judecatii corecte.
De atunci a devenit centrul pentru ingineria electrica, stiinta computerelor, multimea teoriei axiomatice, modul teoretic si pe de alta parte domeniu al stiintei matematicii.
5. Algebre Heyting
O algebra ![]() impreuna cu trei
operatii binare si doua nule este o algebra Heyting daca sunt satisfacute:
impreuna cu trei
operatii binare si doua nule este o algebra Heyting daca sunt satisfacute:
H1: ![]() este o latice
distributiva
este o latice
distributiva
H2: x
x
H3: x x
H4: x y y y
x (x y) x y
H5: x (y z) (x y) (x z)
(x y) z (x z) (y z)
Acestea au fost introduse cu ajutorul lui Birkhoff sub diferite nume algebre Brouwerian si cu diferite notatii (v : u pentru u v).
6. Algebre post n-valuente
O algebra ![]() impreuna cu
doua operatii binare, o operatie unara si doua
operatii nule este o algebra
post n-valuenta daca aceasta satisface fiecare identitate
satisfacuta de algebra Pn=
impreuna cu
doua operatii binare, o operatie unara si doua
operatii nule este o algebra
post n-valuenta daca aceasta satisface fiecare identitate
satisfacuta de algebra Pn=![]() unde
unde ![]() este o multime
total ordonata cu 0<n-1<n-2<..<
2 < 1, si 1′ = 2, 2′ = 3, ., (n-2)′ = n-1,
(n-1)′ = 0 si 0′=1.
este o multime
total ordonata cu 0<n-1<n-2<..<
2 < 1, si 1′ = 2, 2′ = 3, ., (n-2)′ = n-1,
(n-1)′ = 0 si 0′=1.
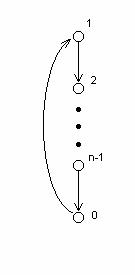
In figura de mai jos operatia
unara "′ " este descrisa cu ajutorul sagetii:
7. Algebre cilindrice de dimensiune n
Daca avem dat nIw, atunci o
algebra (A, ,′, c![]() ,, cn-1, 0, 1, d
,, cn-1, 0, 1, d![]() , d
, d![]() ,, d
,, d![]() ) impreuna cu doua operatii binare, n+1
operatii unare si n2+2 operatii nule este o algebra cilindrica de dimensiune n
daca satisface urmatoarea, unde 0 i, j, k n
) impreuna cu doua operatii binare, n+1
operatii unare si n2+2 operatii nule este o algebra cilindrica de dimensiune n
daca satisface urmatoarea, unde 0 i, j, k n
C1: ![]() este o algebra
Boole
este o algebra
Boole
C2: ci 0
C3: x cix
C4: ci(x ciy) (cix) (ciy)
C5: cicjx cjcix
C6: dii
C7: dik cj (dij djk) daca i j k
C8: ci (dij x) ci (dij x 0 daca i j.
Cilindrul algebric a fost introdus cu ajutorul lui Tarski si Thompson pentru a sustine versiunea algebrica a predicatelor logice.
8. Ortolatici
O algebra ![]() impreuna cu
doua operatii binare, o operatie unara si doua
operatii nule este o ortolatice
daca sunt satisfacute:
impreuna cu
doua operatii binare, o operatie unara si doua
operatii nule este o ortolatice
daca sunt satisfacute:
Q1: ![]() este o latice
marginita
este o latice
marginita
Q2: x x
x x
Q3: (x y)' x' y'
(x y)' x' y'
Q4: (x')' x
O latice ortomodulara este o ortolatice care satisface
Q5: x y x x' y) y.
Observatie: Cand vom afirma ca 'f : A B este morfism' vom subintelege ca A si B sunt universurile a doua algebre de acelasi tip t iar f este morfism de algebre de tip t
. Fiind date
doua grupuri ( G, .
,-1 , 1 ) si ( G′, .
, -1 , 1 ) prin morfism
de grupuri vom intelege o aplicatie f : G G′ astfel incat pentru x, y I G sa avem f ( x y ) = f ( x ) f ( y ), f(x![]() ) = (f (x))
) = (f (x))![]() si f( 1 ) = 1. (Se arata ca pentru ca f
sa fie morfism de grupuri este suficient doar ca f(x y) = f(x) f(y) pentru orice x, y I G).
si f( 1 ) = 1. (Se arata ca pentru ca f
sa fie morfism de grupuri este suficient doar ca f(x y) = f(x) f(y) pentru orice x, y I G).
. Daca (S, ) si (S ) sunt doua semilatici atunci prin morfism de semilatici intelegem o functie f : S S astfel incat pentru orice x, y I S, avem f(x y)=f(x) f(y).
. Daca (L , ) si (L′ , ) sunt doua latici f : L L este morfism de latici daca f ( x y ) = f ( x ) f ( y ) si f (x y) = f (x) f (y) pentru orice x, y I L.
In cazul laticelor marginite prin morfism de latici marginite intelegem un morfism f de latici si care in plus mai verifica conditiile f ( 0 ) = 0 si f ( 1 ) =1
Evident, compunerea a doua morfisme de algebre de acelasi tip este de asemenea morfism.
Despre morfismele i : A B ce sunt injectii, vom spune ca
sunt scufundari iar despre acele morfisme f : A B cu proprietatea ca exista g : B A astfel incat g![]() f = 1A si f
f = 1A si f![]() g = 1B vom spune ca sunt izomorfisme (in care caz vom scrie A B
g = 1B vom spune ca sunt izomorfisme (in care caz vom scrie A B
Se probeaza imediat ca
daca morfismul f : A B este o bijectie, atunci f![]() :B A este de asemenea morfism astfel ca
izomorfismele sunt exact morfismele bijective.
:B A este de asemenea morfism astfel ca
izomorfismele sunt exact morfismele bijective.
Izomorfismele f : A A se zic automorfisme.
Observatie: Pentru doua algebre A si B de acelasi tip, vom nota prin Hom (A, B) multimea morfismelor de la A la B.
Definitia 1.4.
Fie A o algebra de tip t iar B A o submultime nevida a sa. Vom spune
ca B este subalgebra a lui
A daca pentru orice 1 i t) si (b1,b2,...,bn![]() ) I B
) I B![]() avem ca fi(b1,b2,...,bn
avem ca fi(b1,b2,...,bn![]() ) I B.
) I B.
Evident, subalgebrele lui A (impreuna cu restrictiile operatiilor lui A la ele) sunt algebre de acelasi tip t. Daca B A este subalgebra a lui A vom scrie B A.
Daca f : A B este morfism de algebre atunci f (A) este subalgebra a lui B iar daca B A, incluziunea 1B,A : B A este morfism daca si numai daca B este subalgebra a lui A.
Definitia 1.5 Fie A o algebra si S A o multime nevida. Daca exista o cea mai mica subalgebra a lui A (fata de incluziune) ce contine pe S, atunci aceasta se va nota prin [S] si se va numi subalgebra lui A generata de S (elementele lui S se vor numi generatori ai lui A).
Observatie: Daca A si B sunt algebre de acelasi tip, S A este o multime nevida pentru care exista [S], atunci daca f, g : [S] B sunt morfisme astfel incat f S = g S deducem ca f = g.
Sa consideram acum operatorul: Sg : Sub(A) Sub (A), Sg(X) = [X] pentru fiecare X A.
Teorema 1.6. Fiind data o algebra A, atunci operatorul Sg definit mai inainte este un operator algebric de inchidere pe A.
Demonstratie: Faptul ca Sg este operator de inchidere rezulta imediat. Pentru fiecare X A definim: E(X) = X f(a1,..,an) f este o operatie n-ara pe A si a1,.,anIX si recursive En(X) pentru nIN prin E0(X) = X si En+1(X) = E(En(X)).
Cum X E(X) E2(X) deducem ca Sg (X) = X E(X) E2(X) , astfel ca daca a I Sg (X), atunci aIEn (X) pentru un anumit nIN, adica pentru o anumita submultime finita Y X, a I En(Y). Atunci a ISg (Y), adica Sg este un operator algebric de inchidere. g
Corolar 1.7. Daca A este o algebra, atunci LSg (laticea subalgebrelor lui A) este o latice algebrica (vom nota aceasta latice prin Sub [A] pentru a o distinge de laticea Sub (A) a submultimilor lui A).
Teorema1.8. (Birkhoff si Frink) Daca L este o latice algebrica, atunci exista o algebra A astfel incat L sa fie izomorfa cu laticea Sub [A].
Demonstratie: Exista o multime A si un operator algebric de inchidere C pe A astfel incat L Lc.
Pentru fiecare submultime
finita B A si b I C (B) definim o operatie n-ara (n = ![]() ) fB,b pe A
astfel:
) fB,b pe A
astfel:
fB,b(a1, ,an)=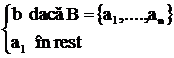
Vom nota tot prin A algebra astfel obtinuta.
Atunci fB, b ( a1, , an ) I C ( ), deci pentru X A, Sg (X) C(X). Pe de alta parte C (X) = si pentru B finita, C(X) = , b I C(B) Sg (B) Sg (X) ceea ce implica C(X) Sg (X), deci C(X) Sg (X). Atunci Lc Sub [A]. g
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |