
Multimi ordonate. Semilatici. Latici (generalitati)
Definitia 3.1. Printr-o multime ordonata intelegem un dublet (A, format dintr-o multime nevida A si o relatie binara pe A notata traditional prin ' ' care este reflexiva, antisimetrica si tranzitiva.Vom spune ca ' ' este o ordine pe A.
Pentru x, y IA vom scrie x < y daca x y x y. Daca relatia ' ' este doar reflexiva si tranzitiva, vom spune despre ea ca este o ordine partiala sau ca (A, este o multime partial ordonata.
Daca pentru x, y I A definim x y daca si numai daca y x obtinem o noua relatie de ordine pe A. Dubletul (A, il vom nota prin As si spunem ca multimea ordonata As este duala multimii A.
Prin A vom desemna o multime ordonata.
Definitia 3.2. Fie m, M I A si S A S
Vom spune ca:
i) m este minorant pentru S daca pentru orice s I S, m s (in caz ca exista, prin inf (S) vom desemna cel mai mare minorant al lui S).
ii) M este majorant pentru S daca M este minorant pentru S in As, adica pentru orice s I S, s M (in caz ca exista, prin sup(S) vom desemna cel mai mic majorant al lui S).
Daca S = A atunci vom nota inf (S) = s1 sn iar sup (S) =s1 sn (evident, in cazul in care acestea exista).
Ordinea ' ' de pe A se zice totala daca pentru orice a, b I A, a b sau b a; o submultime total ordonata a lui A poarta numele de lant.
Pentru a, b I A vom spune ca b urmeaza pe a (sau ca a este urmat de b) daca a < b iar pentru a c b avem a = c sau c = b; vom utiliza in acest caz notatia a b.
Pentru a, b I A vom nota: (a, b) =
[a, b] =
(a, b] =
[a, b) = si
vom numi astfel de submultimi ale lui A intervale (respectiv deschise, inchise, inchise la dreapta si deschise la stanga, inchise la stanga si deschise la dreapta).
Multimile ordonate finite A pot fi reprezentate prin asa-zisele diagrame Hasse. In acest sens, vom reprezenta fiecare element al lui A printru-un cerculet
Daca a b vom desena cerculetul corespunzator lui b deasupra celui ce-l reprezinta pe a, unind cele doua cerculete printr-un segment (de remarcat faptul ca intersectia a doua astfel de segmente poate sa nu reprezinte un element al lui A).
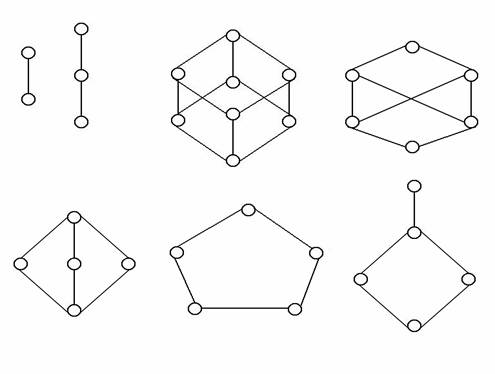
Dintr-o astfel de diagrama putem sa
reconstituim relatia ' tinand cont de observatia ca a < b daca si
numai daca pentru un sir finit de elemente c1, c2,
., cn ale lui A avem a = c1
c2 cn-1 cn = b.
Iata cateva exemple de diagrame Hasse:
Astfel de diagrame sunt greu de utilizat in cazul multimilor ordonate infinite (cum ar fi de exemplu Q sau R cu ordonarea obisnuita).
Fie
( I, ) un lant iar (Ai) iII o familie de multimi ordonate (mutual
disjuncte). Vom nota prin ![]() Ai multimea ordonata ce are drept
multime subiacenta
Ai multimea ordonata ce are drept
multime subiacenta ![]() Ai iar relatia de ordonare este definita
pentru x, y I
Ai iar relatia de ordonare este definita
pentru x, y I ![]() Ai prin x y daca si numai daca xIAi, yIAj si i<j sau Ak iar x y in Ak. Multimea
ordonata
Ai prin x y daca si numai daca xIAi, yIAj si i<j sau Ak iar x y in Ak. Multimea
ordonata ![]() Ai poarta
numele de suma ordinala a
familiei (Ai)iII.
Ai poarta
numele de suma ordinala a
familiei (Ai)iII.
Daca
I= convenim sa notam ![]() Ai = A1
Ai = A1![]() A2
A2![]() .
.![]() An.
An.
Definitia 3.3. Vom spune despre A ca este:
i) inf - semilatice daca pentru oricare doua elemente a, b I A exista a b = inf
ii) sup - semilatice daca pentru oricare doua elemente a, b I A exista a b = sup
iii) latice daca este simultan inf si sup - semilatice (adica pentru oricare doua elemente a, b I A exista a b si a b ).
iv) inf - completa daca pentru orice submultime S A exista inf (S).
v) sup - completa daca pentru orice submultime S A exista sup (S).
vi) completa daca este simultan inf si sub - completa (evident in acest caz se poate utiliza denumirea de latice completa).
vii) inf - marginita daca exista un element notat traditional prin 0 I A astfel incat pentru orice a I A, 0 a.
viii) sup - marginita daca exista un element notat traditional prin 1 I A astfel incat pentru orice a I A, a
ix) marginita daca este simultan inf si sup - marginita (adica 0 a 1 pentru orice a I A). In acest caz 0 se zice element initial (sau prim) al lui A iar 1 element final (sau ultim) al lui A.
x) conditional completa daca pentru orice submultime nevida si marginita S a sa exista inf (S) si sup (S).
Observatii:
1. Orice multime ordonata A care este inf-completa este latice completa.
Intr-adevar, fie M A, M multimea majorantilor lui M iar m = inf(M ). Cum pentru xIM si yIM avem x y deducem ca x m, adica m I M , astfel ca m=sup(M).
2. Daca A este o latice completa, atunci inf ( ) = 1 iar sup (
3. Pentru ca o latice L sa fie conditional completa, este suficient ca pentru orice submultime nevida si marginita S a sa, sa existe doar inf (S) (sau sup (S)).
Definitia 3.4. Un element mIA se zice:
i) minimal daca avand a I A astfel incat a m deducem ca m = a.
ii) maximal daca avand a I A astfel incat m a deducem ca m = a.
Daca A are 0, un element a IA se zice atom daca a 0 si avand x IA astfel incat x a, atunci x = 0 sau x = a (deci 0 < a ).
Definitia 3.5. Daca A este inf-semilatice (respectiv sup-semilatice) vom spune despre o submultime A′ A ca este inf - sub - semilatice (respectiv sup - sub -semilatice) daca pentru oricare doua elemente a, b I A′ deducem ca a b I A′ (respectiv a b I A′ ).
Daca A este latice, A′ A se va zice sub - latice daca pentru oricare doua elemente a, b I A avem ca a b, a b I A′
. Fie N multimea numerelor naturale iar ' ' relatia de divizibilitate pe N. Atunci ' ' este o relatie de ordine pe N. Fata de aceasta ordine N devine latice in care pentru m, n I N , m n = cel mai mare divizor comun al lui m si n iar m n = cel mai mic multiplu comun al lui m si n.
Evident, elementul 1 I N este element initial iar 0 I N este element final.
Aceasta ordonare nu este totala deoarece daca avem doua numere naturale m, n prime intre ele (cum ar fi de exmplu 2 si 3) nu avem nici m n si nici n m .
. Daca K este una din multimile de numere N, Z, Q sau R, atunci K cu ordonare naturala este o latice, iar ordonarea naturala este totala.
. Fie M o multime iar Sub (M) multimea submultimilor lui M. Atunci (Sub(M), ) este o latice completa cu prim si ultim element (respectiv si M).
Fie acum A, A doua multimi ordonate (cand nu este pericol de confuzie convenim sa notam prin ' ' ambele relatii de ordine de pe A si A ) si f : A A o aplicatie.
Definitia 3.6. Vom spune despre f ca este morfism de multimi ordonate (sau aplicatie izotona) daca pentru orice a, b I A cu a b avem f (a) f (b).
Daca A, A sunt inf (sup) - semilatici vom spune despre f ca este morfism de inf (sup)-semilatici daca pentru oricare doua elemente a, b I A, f (a b)=f (a) f(b) (respectiv f ( a b )= f (a) f (b)) .
Daca A, A′ sunt latici, vom spune ca f este morfism de latici daca f este simultan morfism de inf si sup-semilatici (adica pentru oricare doua elemente a, b IA avem f (a b) = f (a) f (b) si f (a b) = f (a) f (b).
Morfismele de inf (sup) - semilatici sunt aplicatii izotone iar daca compunem doua morfisme de acelasi tip obtinem tot un morfism de acelasi tip.
Daca
A, A sunt multimi ordonate iar f : A A este morfism de multimi ordonate, atunci
f se zice izomorfism de multimi
ordonate daca exista g : A A astfel incat f![]() g = 1A si g
g = 1A si g![]() f = 1A.
Acest lucru revine la a spune de fapt ca f este o bijectie. In acest caz vom scrie A A′
f = 1A.
Acest lucru revine la a spune de fapt ca f este o bijectie. In acest caz vom scrie A A′
Analog se definesc notiunile de izomorfism de inf (sup) - semilatici ca si cea de izomorfism de latici.
Definitia 3.7. Fie A o inf - semilatice si F A o submultime nevida a sa.
Vom spune ca F este filtru al lui A daca F este o inf-sub-semilatice si pentru a, bI A, daca a b si a I F atunci b I F.
Vom nota prin F (A) multimea filtrelor lui A.
Notiunea duala celei de filtru este aceea de ideal pentru o sup-semilatice.
Definitia 3.8. Fie A o sub-semilatice iar I A o submultime nevida a sa. Vom spune ca I este un ideal al lui A daca I este sup-sub-semilatice a lui A si pentru orice a, b I A cu a b, daca b I I atunci si a I I.
Vom nota prin I (A) multimea idealelor lui A.
Observatie: Daca A este latice atunci notiunile de filtru si ideal au definitii precise in A (tinand cont ca A este simultan inf si sup-semilatice); evident in acest caz AIF(A) I(A).
Cum intersectia oricarei familii de filtre (ideale) este de asemenea filtru (ideal), putem vorbi de filtrul (idealul) generat de o multime.
Daca A este o inf-semilatie, pentru S A vom nota prin [S) filtrul generat de S (adica intersectia tuturor filtrelor lui A ce contin pe S).
Propozitia 3.9. Daca A este o inf-semilatice si S A o submultime nevida a sa, atunci:
[S) =
Demonstratie: Fie Fs =
Fs I F (A) si S Fs, deci [ S ) Fs.
Daca F I F(A ) astfel incat S F atunci Fs F , deci Fs F = [S), de unde [S)=Fs. g
Daca A este o sup-semilatice iar S A este o submultime nevida a sa, vom nota prin (S] idealul lui A generat de S (adica intersectia idealelor lui A ce contin pe S).
Propozitia 3.10. Daca A este o sup-semilatice si S A este o submultime nevida a sa, atunci:
(S] = . g
Daca A este o inf (sup-semilatice) si a I A, vom nota prin [a) (respectiv (a]) filtrul (idealul) generat de .
Avem ca: [a) = si (a] = . ([a) ((a]) poarta numele de filtrul (idealul) principal generat de a).
Teorema 3.11. Fie ( A , ) o multime ordonata. Atunci A este izomorfa cu o familie de submultimi ale lui A.
Demonstratie: Pentru fiecare a I A consideram Ma = A
Deoarece pentru a,
bIA, a b avem
Definitia 3.12
i) O multime ordonata in care orice submultime nevida a sa are un element initial se zice bine ordonata (evident o multime bine ordonata este inf-completa si total ordonata).
ii) O multime ordonata in care orice submultime total ordonata a sa are un majorant (minorant) se zice inductiv (coinductiv) ordonata.
Pentru orice multime M este verificata axioma alegerii:
Exista o functie s : Sub (M) M astfel incat s (S) I S pentru orice submultime nevida S a lui M.
Lema 3.13. (Bourbaki). Daca (A, ) este o multime nevida, inductiv ordonata si f : A A este o aplicatie astfel incat f(a) a pentru orice a I A, atunci exista uIA astfel incat f (u) = u. g
Corolar 1. (Principiul lui Hansdorf de maximalitate). Orice multime ordonata contine o submultime total ordonata maximala. g
Corolar 2. (Lema lui Zorn). Orice multime nevida inductiv (coinductiv) ordonata are cel putin un element maximal (minimal). g
Corolar 3. (Principiul
elementului maximal (minimal)). Fie (A, ) o multime inductiv (coinductiv)
ordonata si a I A. Exista un element maximal
(minimal) m![]() IA astfel incat a m
IA astfel incat a m![]() (m
(m![]() a). g
a). g
Corolar 4. (Lema lui Kuratowski). Orice submultime total ordonata a unei multimi ordonate este cuprinsa intr-o submultime total ordonata maximala. g
Corolar 5. (Teorema lui Zermelo). Pe orice multime nevida A se poate introduce o ordine fata de care A este bine ordonata. g
Corolar 6. (Principiul inductiei transfinite). Fie ( A, ) o multime bine ordonata infinita si P o proprietate data. Pentru a demonstra ca toate elementele multimii A au proprietatea P este suficient sa demonstram ca:
i) Elementul initial 0 al lui A are proprietatea P.
ii) Daca pentru a I A, toate elementele x I A astfel incat x < a au proprietatea P, atunci si elementul a are proprietatea P. g
Definitia 3.14. Vom spune despre o latice L ca este:
i) modulara daca pentru oricare x, y, z, I L cu z x avem x (y z) = =(x y) z.
ii) distributiva daca verifica una din urmatoarele doua conditii echivalente:
1) x ( y z ) = ( x y ) ( x z ).
2) x ( y z ) = ( x y ) ( x z ) pentru orice x, y, z I L
Orice latice distributiva este modulara, reciproca nefiind adevarata.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |