
Speranta matematica a unei variabile aleatoare discrete.
Fie x o variabila aleatoare discreta a carei lege de distributie este urmatoarea:
![]()
![]()
x x1 x2 x3 ... . xk . .. xn
![]()
P( x = xk ) p1 p2 p3 .......... pk pn
![]()
Definitia 1: Se numeste speranta matematica a variabilei aleatoare discrete x (pe care o notam cu M[x] sau mx) suma tuturor valorilor posibile ale variabilei aleatoare prin probabilitatile respective ale acestor valori
M[x] = x1 p1 + x2 p2 + ..... + xn pn (VII 32)
sau mai simplu:
M[x] = ![]() (VII 33)
(VII 33)
In acest caz avem, dupa cum am mentionat mai sus:
![]() = 1
= 1
Daca valorile variabilei aleatoare formeaza o serie infinita de valori, atunci
Mx = ![]() (VII
34)
(VII
34)
Noi nu vom considera decat variabilele aleatoare pentru care aceasta serie converge. Sa stabilim acum relatia dintre speranta matematica a unei variabile aleatoare si media aritmetica a valorilor variabilei aleatoare pentru un numar mare de probe ; mai exact sa aratam ca pentru un numar mare de probe, media aritmetica a valorilor observate este aproape de speranta matematica sau in virtutea "capitolului 1" putem afirma ca media aritmetica a valorilor observate a unei variabile aleatoare tinde, cand numarul de probe creste nedefinit, spre speranta matematica.
Sa ne imaginam ca efectuam N probe independente. Presupunem ca:
- valoarea x1 se manifesta de n1 ori
- valoarea x2 se manifesta de n2 ori
- valoarea xv se manifesta de nv ori
Variabila aleatoare x ia valorile x1 , x2 , x3 , ....xv
Sa calculam media aritmetica a valorilor obtinute de
variabila x (vom nota
aceasta medie aritmetica prin ![]() [x] sau
[x] sau ![]() ).
).
Avem deci:
![]() =
= ![]() =
=
![]() +
+ ![]() + ...... +
+ ...... + ![]() (VII 35)
(VII 35)
Cum pentru un numar mare de probe N frecventa relativa tinde spre probabilitatea de realizare a valorii xk , avem:
![]()
![]()
Rezulta deci imediat ca:
![]() [x]
[x] ![]() M [x] (VII
36)
M [x] (VII
36)
Remarca 1 Daca am considera schema urnelor cu N
bile, din care n1 bile marcate cu semnul x1
si n2 marcate cu semnul x2
...etc, numarul sperat cand se extrage o bila, va fi dat de forma (34)
altfel spus este egal cu ![]() .
.
Solutia: Variabila aleatoare x poate sa ia valorile :
x1 = 0; x3 = 1; x3 = 2; x4 = 3.
Vom pune intr-un tablou distributia variabilei aleatoare date. Vom gasi probabilitatea acestor valori dupa teorema probelor repetate. (n=3; p = 0,4; q = 0,6)
P( x =
0) = ![]() (0,6)3 = 0,216
(0,6)3 = 0,216
P( x
=1) = ![]() (0,4)(0,6)2 = 0,432
(0,4)(0,6)2 = 0,432
P( x =2) = ![]() (0,4)2(0,6) = 0,288
(0,4)2(0,6) = 0,288
P( x =3) = ![]() (0,4)3 = 0,064
(0,4)3 = 0,064
Tabloul distributiei variabilei aleatoare va fi:
![]() x 0 1 2 3
x 0 1 2 3
![]()
P(x = xk) 0,46 0,432 0,288 0,064
![]()
Vom calcula speranta matematica dupa formula(34).
![]() = 0*0,0216 + 1*0,432 +
2*0,288 + 3*0,064 = 1,2 realizari
= 0*0,0216 + 1*0,432 +
2*0,288 + 3*0,064 = 1,2 realizari
Exemplul 2. Se efectueaza o proba in cursul careia evenimentul A poate sau nu avea loc. Probabilitatea ca evenimentul sa se realizeze este egala cu p. Sa se determine speranta matematica a variabilei aleatoare X exprimand numarul de realizari al evenimentului.
Formam tabloul distributiei variabilei aleatoare:
![]()
![]() x 0 1
x 0 1
![]()
pk 1-p p
![]()
Remarca 2. Se poate stabili in continuare ca speranta matematica M[x] a numarului de realizare a evenimentului A in cursul a n probe independente este egala cu produsul numarului de probe prin probabilitatea p de realizare a evenimentului A in fiecare proba.
M[x]= np (VII 37)
Solutia problemei de la exemplul 1 va fi astfel:
M[x]= n*p = 3.0,4 = 1,2 realizari
Daca in formula (37) se cunoaste M[x] si p, se poate gasi n care este numarul de probe care dau speranta matematicii ceruta de numarul de realizari a evenimentului.
Exemplul 3. Sa se determine speranta matematica a variabilei aleatoare al carui tablou de distributie este urmatorul:
![]() x 1 2 3 . k ..
x 1 2 3 . k ..
![]()
pk p (1-p)p (1-p)2 p .(1-p)k-1 p.
![]()
Solutie: Avem in virtutea relatiei (34) notand cu 1-p = q
mx = 1* p + 2q.p + 3q2p + .... + kqk-1p + .. =
= p(1 + 2q + 3q2 + .. + kqk-1 + .) =
= p(q + q2 + q3 + .... + qk + ...)' =
= p(![]() )' = p
)' = p![]() =
= ![]() =
= ![]() =
= ![]()
Astfel:
mx
= ![]()
Notam ca mx ![]() 1 cand p
1 cand p![]() 1
1
mx ![]()
![]() cand p
cand p![]() 0
0
Se pot explica aceste relatii bazandu-ne pe sensul problemei.
Daca probabilitatea de realizare a evenimentului A este pentru fiecare proba aproape 1 (p ), se poate astepta ca evenimentul A sa aiba loc in cursul unei singure probe (prima) (mx ). Din contra, daca probabilitatea p este mica (p se poate astepta ca pentru realizare sa fie efectuat un numar mare de probe (mx
Se numeste centrul de distributie a probabilitatilor variabilei aleatoare X speranta matematica a variabilei aleatoare X.
Remarca 3: Termenul " centru de distributie a probabilitatilor" este introdus prin analogie cu cel al "centrului de greutate". Daca pe axa 0x se atribuie punctele de abscise x1 , x2 , . ,xn ; masele p1 , p2 , . ,pn se stie de la mecanica teoretica ca centrul de greutate al acestor mase va fi determinata de formula.
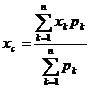 (VII 38)
(VII 38)
Daca
![]()
Atunci
x
c = ![]() (VII
39)
(VII
39)
Formula (39) coincide cu formula sperantei matematice (34).
Am stabilit astfel ca centrul de greutate si speranta matematica se calculeaza cu ajutorul unor formule analoage. Aceasta este motivul pentru care am introdus termenul " centru de distributie a probabilitatilor".
Fie data o variabila aleatoare x cu legea sa de distributie data de figura alaturata: (fig 1). Presupunem ca speranta sa matematica este mx.
P
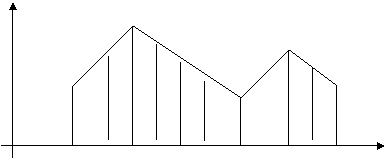
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 X
![]()
![]()
![]()
![]()
![]()
![]()
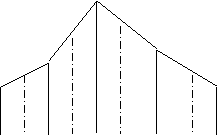
Consideram diferenta intre variabilele aleatoare x si speranta matematica x- mx. Vom numi aceasta variabila centrala sau abatere si o vom nota prin x0.
Este evident ca legea de distributie a acestei variabile aleatoare x0 va fi (cf. fig. 2)

![]()
![]() =
= ![]() -
- ![]()
![]() =
= ![]() -
- ![]() ......
...... ![]() =
= ![]() -
- ![]()
![]()
![]()
![]()
![]() .......
....... ![]()
![]()
Vom gasi speranta matematica a variabilei aleatoare centrala:
M [![]() -
- ![]() ] =
] = ![]() -
- ![]() -
- ![]() =
=
=![]()
![]() =
= ![]() . 1 = 0 (VII 40)
. 1 = 0 (VII 40)
Astfel speranta matematica a unei variabile aleatoare centrale este nula.
Remarca 4. Este util
cateodata sa se considere o variabila nealeatoare (certa)
In acest sens se poate apoi sa se vorbeasca de speranta matematica a unei constante.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |