
Limite de functii. Continuitate. Derivabilitate
. Fie functia
![]() . Calculati derivata
. Calculati derivata ![]() .
.
. Pentru fiecare din functiile date mai jos,
determinati domeniile maxime de definitie si calculati
prima derivata, ![]() :
:
(i).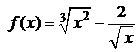 ; (ii).
; (ii). 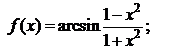 (iii).
(iii).![]() .
.
. Calculati limitele urmatoare:
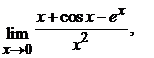
![]()
![]() .
.
Fie ![]() si functia
si functia ![]() , definita prin
, definita prin ![]() . Aratati ca
. Aratati ca
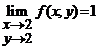 .
.
Solutie. Fie ![]() , oarecare dar fixat. Daca alegem
, oarecare dar fixat. Daca alegem ![]() , atunci pentru
, atunci pentru ![]() si
si ![]() , putem avea (de exemplu, pentru orice
, putem avea (de exemplu, pentru orice ![]() )
) 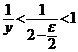 si atunci deducem
si atunci deducem
![]() .
.
Aratati ca 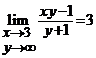 .
.
Solutie. Fie ![]() oarecare. Deoarece
oarecare. Deoarece ![]() , putem alege
, putem alege ![]() si pentru
si pentru ![]() putem scrie
putem scrie
![]() , in orice vecinatate a
punctului
, in orice vecinatate a
punctului
![]() , de forma
, de forma ![]() .
.
Aratati ca functia ![]() , nu are limita in punctul
, nu are limita in punctul ![]() .
.
Solutie. Consideram sirul de puncte ![]() , cand
, cand ![]() . Atunci sirul valorilor
. Atunci sirul valorilor ![]() ,
, ![]() . Alegand un alt sir de puncte, de exemplu, sirul
. Alegand un alt sir de puncte, de exemplu, sirul ![]() , cand
, cand ![]() atunci sirul
valorilor
atunci sirul
valorilor ![]() ,
, ![]() . Asadar, observam ca pentru doua
siruri diferite, care tind catre punctul
. Asadar, observam ca pentru doua
siruri diferite, care tind catre punctul ![]() , atunci se obtin limite diferite, ceea ce contrazice
unicitatea limitei functiei intr-un punct.
, atunci se obtin limite diferite, ceea ce contrazice
unicitatea limitei functiei intr-un punct.
Aratati ca functia 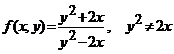 , nu are limita in punctul
, nu are limita in punctul ![]() .
.
Aratati ca 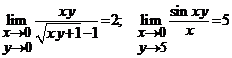 .
.
Solutie. Avem 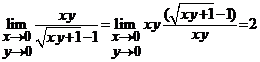 ; Pentru calculul
celei de a doua limita vom folosi limita
; Pentru calculul
celei de a doua limita vom folosi limita ![]() . Avem
. Avem 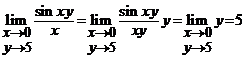 .
.
Fie functia 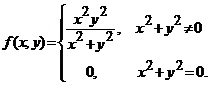 . Sa se arate ca
. Sa se arate ca ![]() este continua pe
este continua pe ![]() .
.
Solutie. In orice punct diferit ![]() ,
, ![]() este continua
deoarece este raport de functii continue. In punctul
este continua
deoarece este raport de functii continue. In punctul ![]() , putem scrie evaluarea
, putem scrie evaluarea
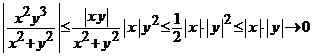 , cand
, cand ![]() .
.
Fie functia 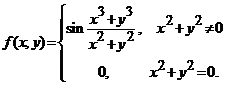 . Sa se arate ca
. Sa se arate ca ![]() este continua pe
este continua pe ![]() .
.
Solutie. In orice punct diferit ![]() , functia
, functia ![]() este continua
deoarece este compunere de functii continue. Din
este continua
deoarece este compunere de functii continue. Din ![]() , deducem ca argumentul functiei
, deducem ca argumentul functiei ![]() , admite majorarea
, admite majorarea
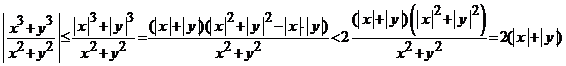 ,
,
Asadar,
avem 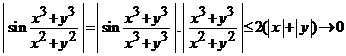 , cand
, cand ![]() , ceea ce arata ca
, ceea ce arata ca ![]() este continua
si in origine.
este continua
si in origine.
Fie functia 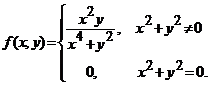 .
.
Sa se arate ca ![]() este continua in
orice punct din
este continua in
orice punct din ![]() , nu este continua in origine, insa restrictia
lui
, nu este continua in origine, insa restrictia
lui ![]() la orice dreapta
la orice dreapta ![]() este continua.
este continua.
Solutie. In orice punct diferit ![]() , functia
, functia ![]() este continua
deoarece este raport de functii continue. Aratam ca in
punctul
este continua
deoarece este raport de functii continue. Aratam ca in
punctul ![]() , functia
, functia ![]() nu are limita.
Intr-adevar, daca alegem directia
nu are limita.
Intr-adevar, daca alegem directia ![]() , atunci avem
, atunci avem ![]() , cand
, cand ![]() . Fie directia
. Fie directia ![]() ,
, ![]() . In lungul acestei directii avem
. In lungul acestei directii avem ![]() si deci,
si deci, ![]() , care arata ca restrictia lui
, care arata ca restrictia lui ![]() la dreptele care trec
prin origine este continua.
la dreptele care trec
prin origine este continua.
Fie functia 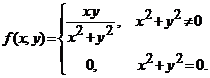 .
.
Sa se arate ca ![]() este continua in
orice punct din
este continua in
orice punct din ![]() , este discontinua in origine, insa este
continua in raport cu fiecare variabila.
, este discontinua in origine, insa este
continua in raport cu fiecare variabila.
Solutie. In orice punct diferit ![]() , functia
, functia ![]() este continua
deoarece este raport de functii continue. In punctul
este continua
deoarece este raport de functii continue. In punctul ![]() , functia
, functia ![]() nu are limita
deoarece daca alegem, de exemplu, directia
nu are limita
deoarece daca alegem, de exemplu, directia ![]() ,
, ![]() , atunci in lungul acestei directii avem
, atunci in lungul acestei directii avem ![]() si deci, valorile
lui
si deci, valorile
lui ![]() depind de
directia aleasa, ceea ce arata ca functia
depind de
directia aleasa, ceea ce arata ca functia ![]() nu are limita
unica in punctul
nu are limita
unica in punctul ![]() . Asadar, cand
. Asadar, cand ![]() , nu exista limita
, nu exista limita 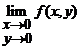 .
.
Avem 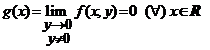 si
si 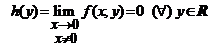 si atunci
limitele iterate sunt egale:
si atunci
limitele iterate sunt egale:
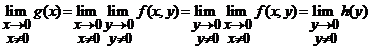 .
.
Fie functia 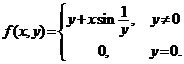 .
.
Sa se arate ca ![]() are limita in
punctul
are limita in
punctul![]() , nu exista limita iterata
, nu exista limita iterata ![]() insa limita
iterata
insa limita
iterata ![]() exista si
este egala cu zero.
exista si
este egala cu zero.
Solutie. Avem pentru ![]() , putem scrie
, putem scrie
![]() , cand
, cand ![]() ;
; 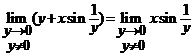 , care evident nu exista si
, care evident nu exista si 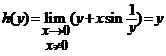 ;
;
Asadar,
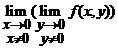 nu exista,
insa
nu exista,
insa 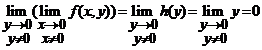 .
.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |